ETH-状态树
约 9644 字大约 32 分钟
2021-10-13
相关术语
tansaction-based ledger 基于交易的账本
account-based ledger 基于账户的账本
balance 余额
nonce 交易次数
code 代码
storage 存储
merkle proof merkle证明
immutable 不可修改的
trie 前缀树或字典树
branching factor 分叉系数
Bloom bloom filter 布隆过滤器
gas 汽油费
external block 以太坊实际传输区块结构
RLP(recursive length prefix) 极简的序列化协议
protocal buffer 序列化库
nested array of bytes 嵌套字节数组
了解一下以太坊是用什么样的数据结构来实现的acount-based ledger。
如何实现从账户地址到账户状态的映射addr->state。以太坊中用到的地址是160bits的,也就是20个字节(1字节等于8位,所以160位除以8等于20字节),一般表示成40个16进制的数(0~f)。这个状态就是外部账户和合约账户的状态,包括余额balance、交易次数nonce,对于合约账户还包括代码code、和存储storage。那么采用什么样的数据结构来实现这个映射呢。
哈希表
直观来看,比较像key-value pair,给定一个地址,找到一个状态。所以一个比较直观的想法,就用一个哈希表实现。就是系统中的全节点维护一个哈希表,每次有一个新的账户,就插入到哈希表里么。要查询账户的余额,就直接在哈希表中查询。如果不考虑哈希碰撞的话,查询的效率即便是常数时间内完成的,修改也是很高效的。
这样有什么问题呢?
使用哈希表的话,如果需要提供merkle proof,怎么提供?比如给某个人签合同,希望他能证明一下他有多少钱,证明一下账户余额。
一种方法是,把这个哈希表中的元素组织成一个merkle tree,然后算出一个根哈希值,这个根哈希值要保存在block header里,就像比特币中也有merkle tree,根哈希值,保存在block header中公布出去。根哈希值只要是正确的,就能保证树不会被篡改。这种方式的问题是,如果有新区块发布,新区块包含有新的交易,就必然会使得哈希表的内容发生变化,然后把哈希表中的内容再重新组织成merkle tree么?这样的代价就太多了。因为实际上,真正发生变化的只是一小部分。因为只有那个区块里所包含的交易所关联的账户才会发生变化,大部分账户的状态是不变的,所以每次都重新构建一个merkle tree,代价就太大了。
那么比特币中每构建一个区块,不是也要构建一个merkle tree么,那个为什么没问题?因为比特币的区块中的merkle tree是每个区块的,下次构建新的区块再构建新的merkle tree,是不可修改的immutable。区块里包含的交易也是有上限的,一个区块包含最多4000个交易,很多区块里面都到不了4000个。
而以太坊的账户的状态,是要把所有的账户一起构建成merkle tree,这个要比比特币一个区块构建的merkle tree,要高好几个数量级。除了提供merkle proof外,merkle tree还有另外一个重要的作用,维护各个全节点之间状态的一致性,如果没有把这个根哈希值发布出来,每个节点在本地维护一个数据结构,怎么知道你的数据结构的状态根别人的是否一致呢?所以,各个全节点要保持状态的一致才行。这也是为什么比特币中,把根哈希值写在块头的一个原因。
所以这种方案是不行的。
回顾merkle proof
Merkle证明(Merkle Proof),也称为Merkle路径,是一种用于验证区块链中某一特定交易确实存在于某一区块内的机制。这一机制是基于Merkle树(Merkle Tree)的结构来进行的。下面是对Merkle证明的详细介绍:
什么是Merkle证明? Merkle证明是一种数据完整性验证方法,它允许用户通过提供Merkle路径来证明某个数据项存在于Merkle树中。在区块链中,Merkle证明被用来验证交易的有效性和来源。每个交易都有一个与之对应的Merkle路径,通过这个路径可以追溯到交易在Merkle树中的位置,从而证明该交易是来自区块链的真实有效交易。
Merkle证明的工作原理
- 构建Merkle树:Merkle树的每个叶节点是某个交易的哈希值,每个非叶节点是其子节点哈希值合并后再哈希的结果,最终形成一个根哈希值,代表了所有底层数据的完整摘要。
- 验证步骤:
- 找到交易哈希:首先,你需要知道你想要验证的交易的哈希值。
- 获取路径(Merkle Path):从该交易的哈希开始,找到一条路径通向Merkle树的根。这个路径上会有一系列的哈希值,这些哈希值是用于从叶节点(你的交易)计算到根节点的。
- 重新计算并比对根哈希:使用这些路径上的哈希值和给定的交易哈希,通过相同的哈希函数重新计算出一个根哈希。
- 验证根哈希:如果重新计算出的根哈希与区块头中存储的默克尔根相匹配,那么这个交易就被认为是存在于该区块内的。
Merkle证明的应用
- 数据完整性验证:通过Merkle Root,可以快速验证某个数据块是否在树中。
- 数据一致性检查:通过对比不同设备上的Merkle Root来判断数据是否一致。
- 高效:只需提供叶子节点的哈希值及其验证路径即可证明数据的完整性,而无需提供所有数据块。
优点与缺点
- 优点:Merkle树能够以一个简短的方式证明一棵树中存在某一个元素,大大提高了数据验证的效率和可扩展性。
- 缺点:Merkle树只能保证交易数据的完整性和真实性,无法防止恶意节点的攻击。
Merkle证明是区块链技术中确保数据完整性和安全性的关键组成部分,它通过提供一种高效的方式来验证交易的存在性和完整性。
以及merkle non-proof
- Merkle树不支持直接的非成员证明:传统的Merkle树并不直接提供非成员证明的功能。
- 非成员证明的实现:要实现非成员证明,一种方法是通过提供两个邻居节点的Merkle证明,这两个节点分别位于所要证明不存在的元素的两侧。如果这两个证明都是有效的,并且它们是邻居,那么就可以证明给定的键(key)不存在于Merkle树中。
- 复杂度问题:如果Merkle树未排序,证明非成员的复杂度为O(n),这意味着需要检查树中的每个节点。但是,如果采用排序的Merkle树,可以通过查找非成员元素相邻的两个叶子节点,并证明这两个叶子节点是邻居,来证明非成员元素不存在于排序的Merkle树中,这样复杂度可以降低。
总结来说,Merkle非成员证明是一种证明数据项不存在于Merkle树中的机制,它在需要验证数据完整性和存在性的场景中非常有用,尤其是在区块链和分布式系统中。通过特定的数据结构和算法,可以在一定程度上实现非成员证明,尽管这可能涉及到较高的计算复杂度。
merkle tree
直接就用一棵merkle tree,把所有的账户放进去。要给的时候,直接在merkle tree里改。
这样有什么问题呢?
这个方法的问题在于,merkle tree没有提供一个高效的查找和更新的方法。
想想比特币的merkle tree是怎么做的,最下层叶子节点是tx(transaction交易),然后取哈希值,俩俩结合,再取哈希值,再结合,从下往上构成。它没有提供快速查找和更新的方法,那是因为比特币不需要。
还有一个问题,如果所有账户放在一个merkle tree,这个merkle tree要不要排序sorted merkle tree?就像上面merkle non-proof提到的,如果不排序,没有办法证明merkle non-proof也就是non-membership。merkle tree要证明一个交易包含在区块里是不需要排序的,要证明一个交易没有包含在区块里是需要排序的。
不排序还有另外一个问题,这些账户组成的merkle tree,叶子节点存储的是账户的信息,如果不规定在叶子节点出现的顺序,那么这样构建出来的merkle tree不是唯一的。每个节点构建的merkle tree如果不排序,是不一样的,算出的根哈希值也是不一样的。
比特币中的merkle tree也是不排序的,为什么没有这个问题?因为比特币中每个全节点收到的交易也是不一样的,理论上来说构建出来的根哈希值也是不一样的。但是比特币有个重要的区别,只有最后获得记账权的那个节点说的才算,也就是唯一的,其他节点虽然构建的不一样,但是没有挖到矿就没有话语权。
sorted merkle tree
那么用排序的如何呢?
也有问题,比如新增一个用户,账户地址是随机的,它在叶子节点中的位置很可能是插在中间的。那后面的结构都得变,插入代价太大了!
MPT
所以简单的数据结构是不行的,以太坊其实采用的是MPT,Merkle Patricia Tree。
在了解MPT之前,先来掌握一下trie,又称为前缀树或字典树,也是key value的存储。英文中信息检索retrieval,从这中间取了4个词取位tire。
tire
比如说有几个单词: general, genesis, god, go, good。
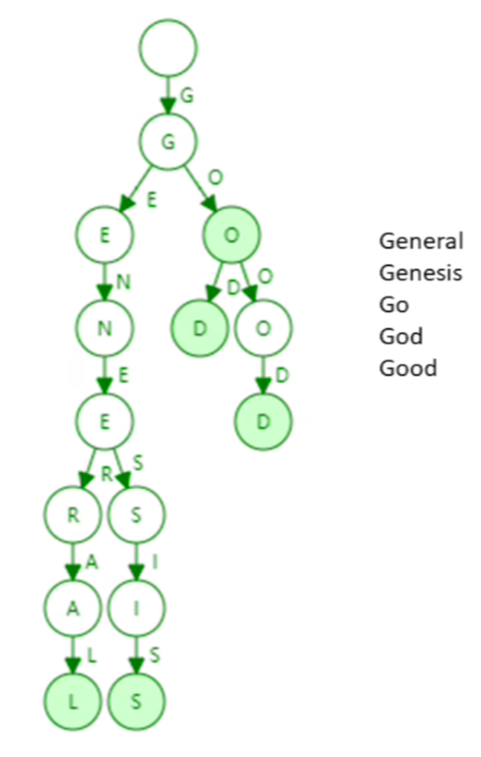
之前提高过,地址是表示成40个16进制的数。所以这个分叉数管他叫branching factor 分叉系数。是17,因为是16进制0到f,再加一个结束标志符,所以是17。
还有特点,trie的查找效率取决于key的长度,key越长,查找需要访问内存的次数就越多。当前应用场景的key有多长呢,都是一样长的,都是40!因为地址都是40位16进制的数。
提示
要计算40个16进制数的总长度是多少位,我们需要理解16进制数与位之间的关系。
- 每个16进制数可以表示4位二进制数,因为16=24。
- 因此,每个16进制数的长度是4位。
所以,40个16进制数的总长度是: 40×4=160 位40×4=160 位
另外比特币和以太坊的地址是不通用的,格式、地址都是不一样的。 当然以太坊的地址也是公钥转换来的,其实就是公钥取hash,然后签名截一段,只要后面160位,就得到了地址。
第三个特点。如果采用哈希表来存储这个key value。从理论上来说,是有可能出现哈希碰撞的,而trie是不会出现碰撞的。
第四个特点。前面提到如果merkle tree不排序的话,账户插入到树中,得到的结果是不一致的的。而trie是一致的!
第五个特点。跟更新相关。每发布一个区块,系统中绝大多数状态是不变的,只有个别收到影响的账户才会变。所以它具有更新操作的局部性!!比如上图的中,想要更新genesis这个key对应的value,这个图是只画出了key,没有画出value。只用访问下面的分支即可,其他分支是不用访问的,也不用遍历整棵树。
所以这么多优点的东西,它的缺点呢?像图中左侧,都只有一个子节点,“一脉单传“的形式,增加了存储和查询的开销。如果能够合并部分,不但等节省存储的开销,同时也能提高查找的效率,不用一次一个的往下找。这就引入了Patricia tree,或者叫Patricia trie。
Tire
Trie,又称为前缀树或字典树,是一种树形数据结构,用于存储动态集合中的字符串,并且能够高效地检索信息。Trie的每个节点代表一个字符,从根节点到某一节点的路径表示一个字符串中的前缀。以下是Trie的一些关键特性和应用:
Trie的基本结构
- 节点:Trie的每个节点代表一个字符,可以是任意的字符集,例如字母、数字或字节。
- 边:节点之间的连接表示字符之间的顺序关系。
- 结束标记:通常,一个节点会有标记来表示该节点是否是一个单词的结束,这在存储字符串集合时特别有用。
Trie的工作原理
- 插入:插入一个字符串时,从根节点开始,对于字符串中的每个字符,如果相应的子节点不存在,则创建新节点。如果字符串已经存在于Trie中,则在最后一个字符的节点上标记结束。
- 搜索:搜索一个字符串时,从根节点开始,按照字符串的字符顺序遍历节点。如果某个字符的节点不存在,则表示字符串不在Trie中。
- 删除:删除操作稍微复杂,需要递归地删除节点,同时确保不删除其他字符串共享的部分。
- 遍历:Trie可以方便地进行前缀遍历,这在自动补全和拼写检查等应用中非常有用。
Trie的优点
- 快速检索:Trie可以在O(m)的时间复杂度内完成插入、搜索和删除操作,其中m是字符串的长度。
- 节省空间:由于共同前缀的共享,Trie可以比分别存储每个字符串节省空间。
- 动态更新:Trie可以动态地插入和删除字符串,适合需要频繁更新的场景。
Trie的应用场景
- 自动补全:在搜索引擎、命令行界面等场景中,Trie可以快速提供基于当前输入的补全建议。
- 拼写检查:Trie可以用来快速检查拼写错误,并提供正确的拼写建议。
- IP路由:在网络路由中,Trie可以用来快速匹配和查找IP地址。
- 基因序列分析:在生物信息学中,Trie可以用来存储和检索DNA、RNA序列。
Trie的变种
- Compressed Trie(压缩Trie):也称为Radix树,当多个节点只有一个孩子时,可以合并这些节点以节省空间。
- Patricia Trie( Patricia树):是一种特殊的Trie,其中每个节点(除了根节点)都是一个非叶子节点,并且每个节点至少有两个子节点。这种结构确保了树的宽度,进一步节省了空间。
Trie是一种非常强大的数据结构,特别适合于处理字符串集合,它在许多需要快速检索和动态更新的场景中都有广泛的应用。
Patricia tree
一种经过路径压缩的trie。
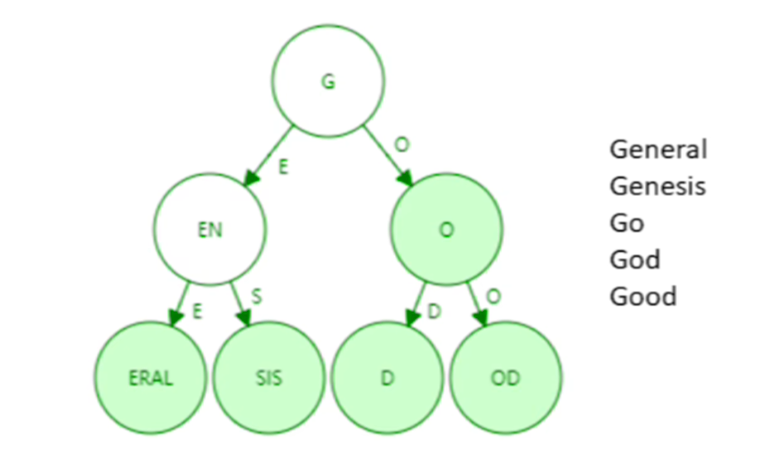
还是那几个单词。但是经过压缩后,直观上树的高度明显缩短了,这样访问内存的次数大大减少了,效率就提高了。但是要注意一点,如果插入新的单词,原来压缩的路径,可能会扩展开来。
路径压缩在什么情况下效果明显呢?因为确实有些例子效果可能不明显。看一下下面的。
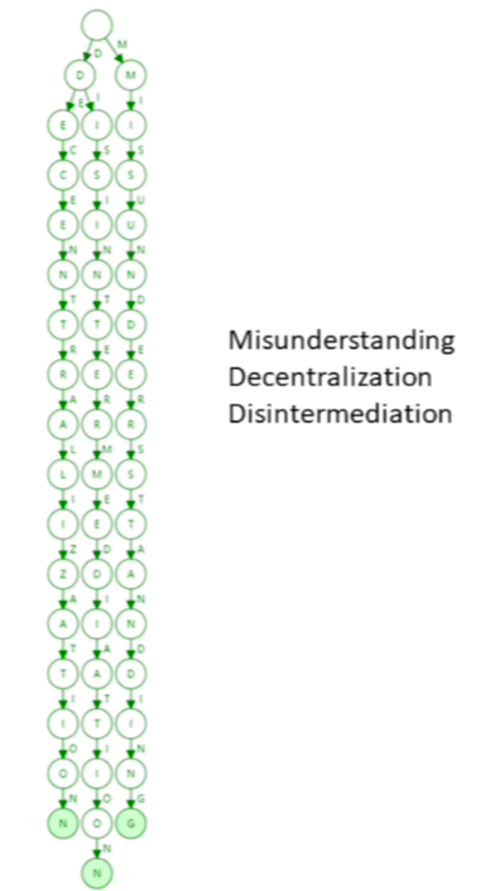
这么做效率就不大,快退化成线了,更别谈什么高效了。 如果用Patricia trie会是怎么样的?
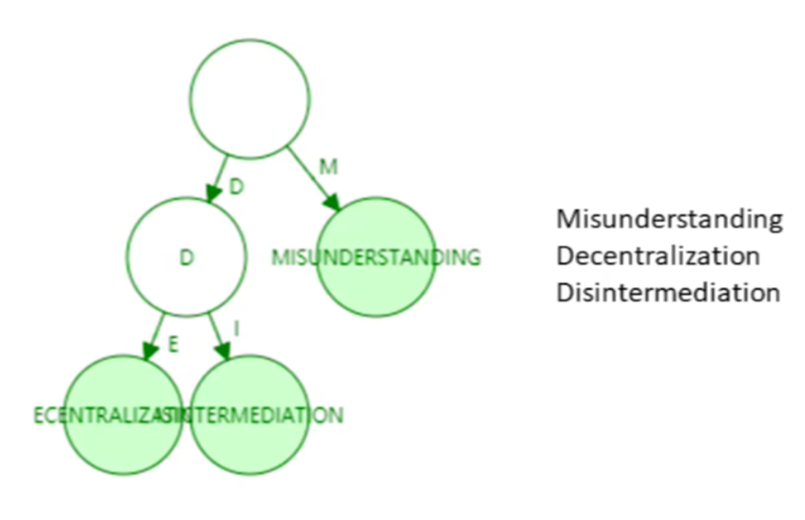
这个树的高度是明显变低了。所以键值分布比较稀疏的情况,路径压缩效果比较好!!那么我们这个键值分布是不是稀疏的呢?键addr是地址160bits的,2160个可能,这是一个非常非常大的数。非常非常稀疏。
为什么要设置的稀疏呢?其实就是为了防碰撞。以太坊的普通账户和比特币是一样的,本地生成一个公私钥对就完事了,所以要范围足够大。这样设置可能看着比较浪费,但是这是去中心化的系统防止账户冲突的唯一办法。
patricia trie
Patricia Trie,也称为压缩前缀树(Compressed Prefix Tree),是一种特殊的Trie树,它通过压缩具有相同前缀的节点来优化存储空间和提高检索效率。以下是Patricia Trie的一些关键特点和工作原理:
- 压缩机制:在Patricia Trie中,如果一个节点只有一个子节点,那么这个子节点将与父节点合并,直到存在多个子节点或到达叶子节点。这种压缩机制使得树更加紧凑,减少了节点数量,从而提高了空间效率。
- 键的存储:Patricia Trie中的每个节点存储的是一个键的前缀,而不是单独的字符或字节。这意味着节点可以表示多个键的共同前缀,进一步减少了存储需求。
- 路径表示:在Patricia Trie中,从根节点到叶节点的路径代表了键的编码。这种路径编码允许快速地确定键是否存在于树中,并且可以快速地进行插入和删除操作。
- 快速检索:由于Patricia Trie的压缩特性,它在检索时可以快速跳过共享前缀的节点,这使得它在处理大量具有共同前缀的键时特别有效。
- 应用场景:Patricia Trie因其高效的字符串处理能力,被广泛应用于需要快速检索的场景,如IP地址路由、搜索引擎优化、实时数据分析、字典或输入法的自动补全功能等。
- 字节级别的前缀匹配:Patricia Trie通过将字符串拆分成字节序列并按照位进行比较,实现了字节级别的前缀匹配,这使得查找过程可以在较短的时间内完成。
- 排序和遍历:由于Patricia Trie的结构特性,它支持按键排序和有序遍历,这对于需要按顺序处理数据的应用非常有用。
- 灵活性:Patricia Trie的键值对可以是任何可进行位操作的对象,不仅限于字符串,这增加了它的灵活性和应用范围。
总的来说,Patricia Trie是一种高效的字符串查找数据结构,它通过压缩共享前缀的节点来优化存储和检索效率,特别适用于需要处理大量字符串数据的场景。
那Patricia trie已经很优秀了,MPT是干嘛的呢。
merkle patricia tree
merkle tree和binary tree有什么区别?把普通指针换成了哈希指针。
merkle patricia tree和patricia tree也是同样,把普通指针换成了哈希指针。
所以所用账户组成一棵MPT,用路径压缩提高效率,然后把普通指针换成哈希指针。就可以计算出一个根哈希值。这个根哈希值也是写在block header里面的。
比特币的block header里只包含一个哈希值,就是区块里所有交易组成的merkle tree的根哈希值。 以太坊中有三个,也有关于交易的交易树,现在讲的是关于账户的状态树,以及收据树。
那么以太坊这个根哈希值有什么用。
第一,是防止篡改。
第二,merkle proof。
第三,就像sorted merkle tree一样,也可以证明non-membership问题。
merkle patricia trie
Merkle Patricia Trie(MPT)是一种结合了Merkle树和Patricia Trie的数据结构,它在以太坊中扮演着至关重要的角色。以下是Merkle Patricia Trie的一些关键特性和应用:
- 数据存储:MPT用于存储以太坊中的所有账户状态、合约代码和存储数据。每个账户地址都是一个键,账户状态(余额、nonce等)是值。
- 数据完整性验证:MPT通过Merkle树的特性,允许快速验证数据的完整性,无需下载整个数据库。任何数据的修改都会导致Merkle根哈希值的改变,从而保证数据的防篡改性。
- 高效的查找、插入和删除操作:Patricia Trie的前缀压缩特性极大地减少了存储空间和查找时间。
- 防篡改:MPT的任何数据修改都会导致Merkle根哈希值的改变,从而保证数据的防篡改性。
- 轻客户端验证:轻客户端不需要下载完整的区块链数据,只需要下载区块头和MPT的根哈希值。通过验证根哈希值,轻客户端可以验证交易的有效性,而无需下载完整的区块数据,从而节省了带宽和存储空间。
- 智能合约存储:智能合约的存储数据也存储在MPT中,这保证了智能合约数据的完整性和安全性。
- 工作原理:MPT的核心思想是将键值对存储在Trie中,并通过哈希运算生成Merkle根哈希。任何对Trie的修改都会导致根哈希值的改变。
- 安全性增强:MPT针对传统Trie的缺点进行了改进,主要体现在数据完整性、防篡改能力和验证效率的提升。
- 应用场景:MPT被广泛应用于以太坊状态存储和其他分布式账本技术中,用于存储数据并实现数据防篡改和高效验证。
- 未来展望:随着以太坊技术的不断发展,MPT的应用范围和优化策略也在不断演进,未来可能会包括更高级的压缩算法、分布式Trie和基于硬件加速的Trie。
总的来说,Merkle Patricia Trie是一种高效、安全、可靠的数据结构,它在以太坊中用于存储和管理海量的账户数据,并确保区块链数据的可靠性和安全性。
modified MPT
modified merkle patricia tree,
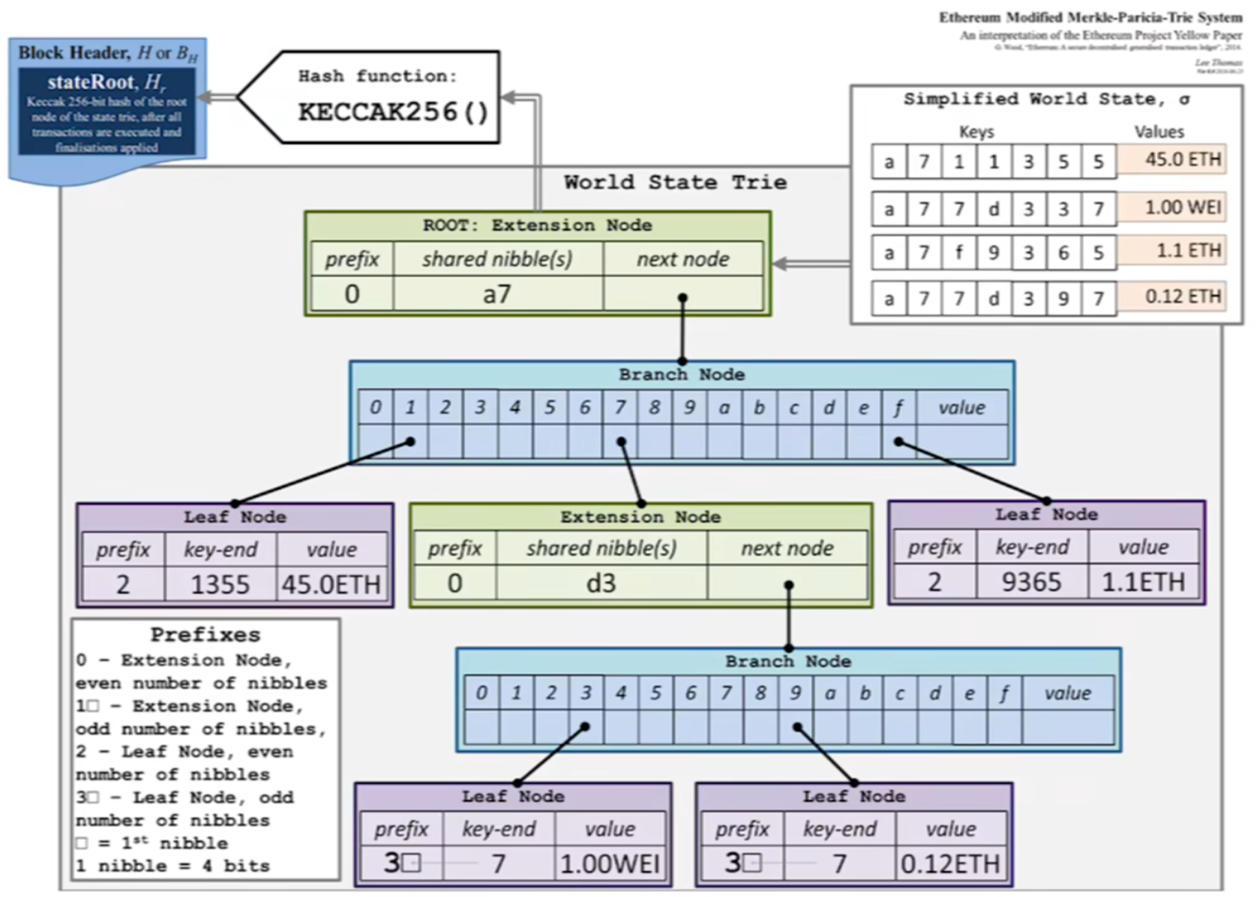
modified merkle patricia tree
Modified Merkle Patricia Tree(MPT)是一种在区块链技术中,尤其是在以太坊中使用的数据结构。它结合了Merkle树的安全性和Patricia Trie的效率,用于存储和验证数据。MPT中的节点类型包括:
- NULL节点:表示空值或空路径,用于表示树中的空节点。
- 分支节点(Branch Node):包含17个元素的节点,结构为v0…v15,vtv0…v15,vt,其中v0v0到v15v15对应于可能的16个分支,而vtvt是值节点,用于存储键值对的值。
- 叶子节点(Leaf Node):包含两个元素,编码路径(encodedPath)和值(value)。叶子节点用于存储具体的数据信息,通常是账户余额或智能合约代码。
- 扩展节点(Extension Node):也包含两个元素,编码路径(encodedPath)和键(key)。扩展节点用于链接其他节点,其中encodedPath包含了要跳过的部分路径,key用于下一次数据库查询。
MPT的优化包括路径压缩,通过合并公共路径有效减少存储空间,提高查询效率。叶子节点和扩展节点都使用encodedPath,但它们之间的区别在于叶子节点存储的是值,而扩展节点存储的是指向下一个节点的键或哈希。
叶子节点的encodedPath编码了路径剩余的片段,可以直接查询值。这种结构使得MPT在存储和检索数据时非常高效,尤其是在处理大量具有共同前缀的键时。
MPT的安全性来自于其Merkle树的特性,任何数据的更改都会影响到树的哈希,从而提供数据完整性验证的保障。这种结构不仅提高了数据检索的效率,还确保了数据的安全性和完整性,使其成为区块链技术中理想的数据存储解决方案。
以太坊中MPT的实现
每次发布一个新的区块时候,这个状态树的有一些节点的值会发生变化,这些改变不是在原地改的。而是新建一些分支,原来的状态是其实是保留下来的。
这是俩个相邻的区块,左侧区块State Root就是状态树的根哈希值,下面显示的是这棵树。右侧区块的State Root是新的区块的状态树。 可以看到,虽然每个区块有一个状态树,但是大部分节点是共享的(图中右侧区块State Root关联了左侧区块State Root所关联的树)!向右边State Root主要都是指向左边这棵树的节点。只有那些发生的改变的节点,是需要新建一个分支的。这个账户是个合约账户,因为它有code还有storage。所以合约账户的存储也是用MPT的形式保存下来的。
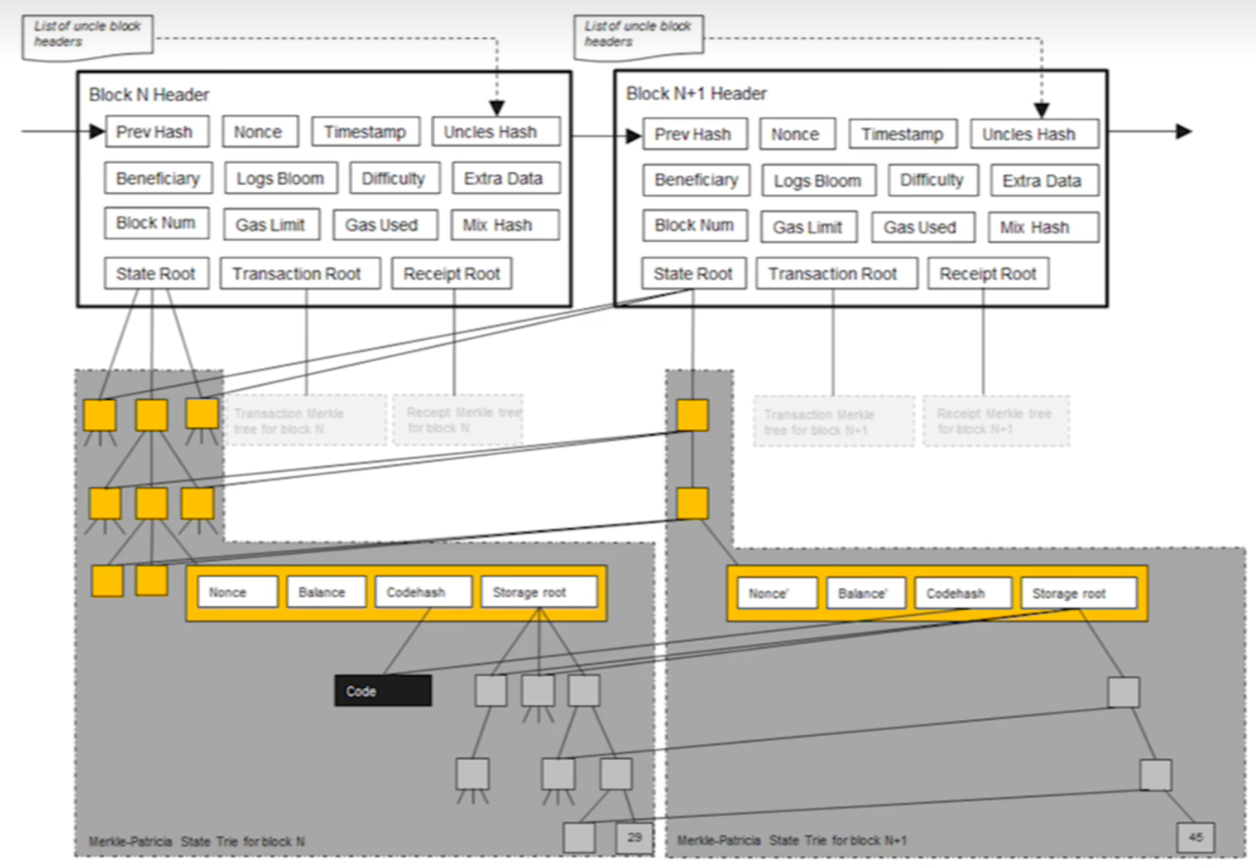
这个存储是什么?其实也是key value的storage。所以以太坊的数据结构是一个大的MPT包含很多小的MPT。每一个合约账户的存储都是一个小的MPT。
所以,系统在每个全节点需要维护的不是一棵MPT,而是每次出现一个区块,都要新建一个MPT,只不过这些状态树中大部分的节点是共享的。只有少数变化的节点需要新建分支。
为什么要保存历史状态,不在原地直接改了,而是新建分支?
系统中有的时候会出现分叉,临时性分叉其实是很普遍的。以太坊把出块时间降到十几秒,这种临时性的分叉是一种常态,因为区块在网上传播时间也是需要很多秒的。假设有一个分叉,比如说上一个节点胜出了,下面分叉节点该怎么办? 回滚roll back么? 接受了下面分叉区块的状态要取消掉,退回上一个区块的状态。就是有的时候,可能需要把当前状态退回到处理到这个区块的前一个的状态。
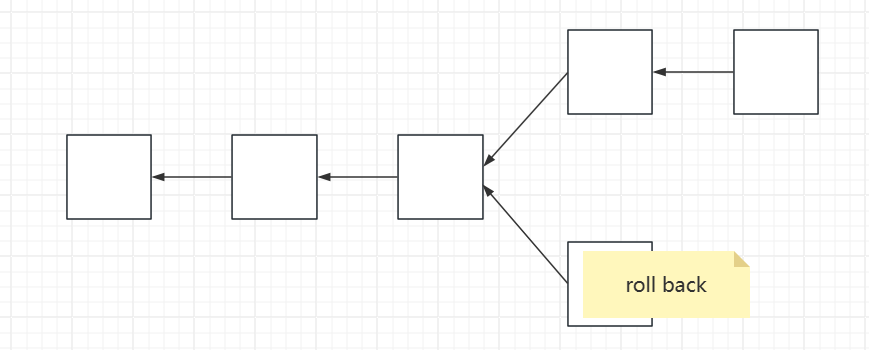
那如何实现回滚呢,就是要为何这些历史纪录。不是说留着历史证明自己以前有多少钱,而是要留着这些交易,有可能要undo。这个跟比特币还不太一样,比比特币简单,有的时候可以通过反向操作,推算出前一个状态。以太坊中为什么不行?因为以太坊中有智能合约,以太坊中智能合约是图灵完备的,它编程功能是很强的,从理论上来说可以实现很复杂的功能,跟比特币那种简单的脚本不一样。所以以太坊中不保存以前的状态,智能合约执行完之后,想在推算出之前是什么状态,是不可能的,谁知道合约内部代码是怎么做的。
所以要想支持回滚,必须得保存历史状态。
structure
header

- Root 状态树的根哈希值
- TxHash 交易树的根哈希值
- ReceiptHash 收据树的根哈希值
- Bloom bloom filter,布隆过滤器,提供一种高效的查询符合某种条件的交易的执行结果
- Difficulty 挖矿难度,也是会调整的
- gas 汽油费,智能合约要消耗汽油费,类似比特币交易费
- MixDigest 挖矿相关,是这个随机数经过一些计算算出的hash值
- nonce 挖矿相关,随机数
body
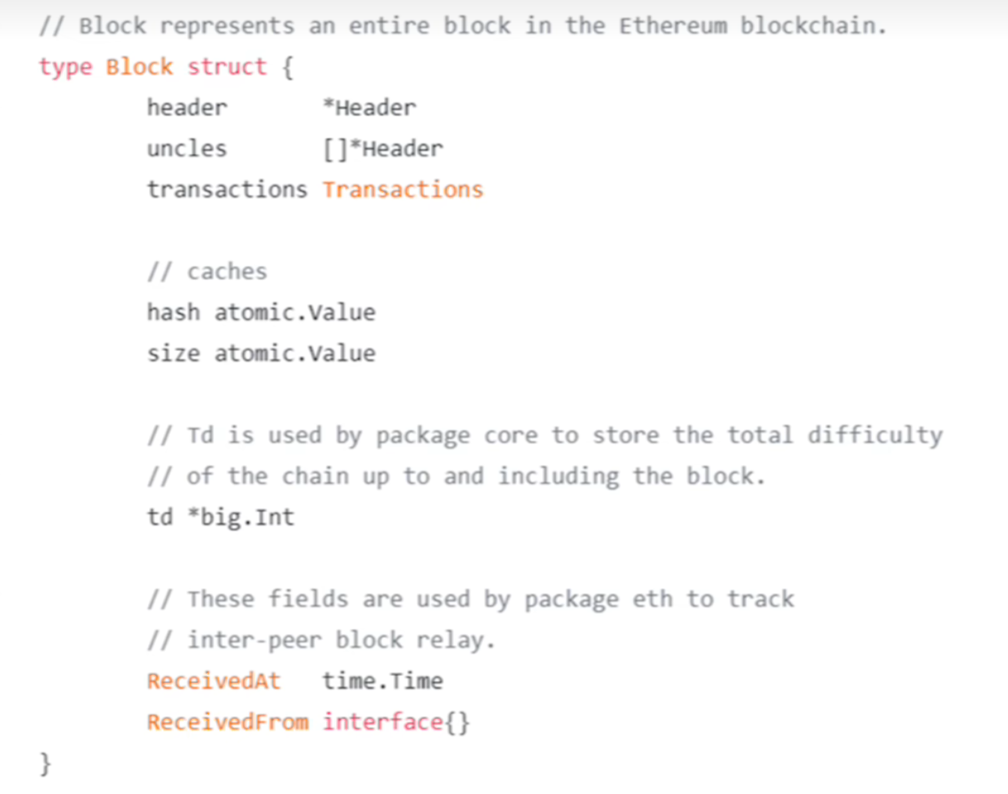
- header 就是上面
block header的指针 - uncles 就是上面叔父区块
header的指针,可是是多个,是数组 - transactions 交易列表
extblock
external block其实这才是区块在网上发布的时候,发布的就是这些信息。就是前面block body中的前三项的各种指针。

RLP
状态树中保存的是key value pair。key就是地址,到这里为止,主要讲的就是这个键值,地址的管理方式。那么value呢,这个账户的状态呢?是怎么存储在状态树当中呢?
实际上是要经过一个序列化过程的,RLP(recursive length prefix),用这个编码做序列化。这个序列化方法特点就是简单,极简主义的。protocal buffer简称protobuf是一个很有名的做序列化的库,跟这个库相比,RLP就是越简单越好。它只支持一种类型,nested array of bytes,字节数组,可以嵌套。以太坊中所有的其他类型,整数也好,比较复杂的哈希表也好,最后都要变成nested array of bytes,所以要实现一个RLP,比实现protobuf要简单的多。因为难的东西它都不做,都推给应用层。。
RLP
递归长度前缀(Recursive Length Prefix,简称RLP)编码是以太坊中用于序列化数据的主要方法,它能够将复杂的数据结构编码成字节序列,以便于网络传输和存储。以下是RLP的一些关键特性和规则:
- 适用性:RLP用于编码任意嵌套的二进制数据数组,特别适用于以太坊中的数据序列化。
- 数据类型简化:RLP只定义了两种类型的数据:字符串(byte数组)和字符串的数组(即列表)。
- 编码规则:RLP的编码规则包括:
- 规则一:对于值在[0, 127]之间的单个字节,其编码是其本身;无需前缀。
- 规则二:如果字符串的长度为0-55个字节之间,编码的结果是数组本身,再加上
0x80加上字符串长度作为前缀。 - 规则三:如果字符串(数组)长度大于55字节,编码结果第一个值是
0xb8加上字符串长度所占用的字节数,然后是数组长度本身的编码,最后是byte数组的编码。 - 规则四:对于列表的编码,如果列表的总长度小于56字节,前缀是
0xc0加上列表长度;如果列表总长度大于55字节,前缀是0xf7加上列表长度所占字节数,接着是列表长度的编码,最后是列表中每个元素的编码。
- 大端序二进制形式:RLP要求整数以不带前导零的大端二进制形式表示,这意味着整数值零相当于空字节数组。
- 数据结构编码:RLP的主要目标是解决结构体的编码问题,而对原子数据类型的编码则交给更高层的协议。
- 应用场景:RLP在以太坊生态系统中的应用广泛,从交易信息的构建、智能合约的状态管理,到链上数据的存储与传输,几乎在每个需要处理复杂数据结构的地方都能见到它的身影。
- 跨平台兼容性:RLP可以在多种环境中运行,包括服务器端的Node.js和前端浏览器环境。
- 编码效率:RLP优化的算法保障了数据转换的效率,特别适合处理大规模数据结构。
- 社区支持:RLP库由活跃的以太坊JS社区维护,获得持续的更新和专业的问题解答。
RLP编码是理解和使用以太坊技术的基础,它为以太坊提供了一种高效、灵活且可靠的数据编码方式。
protobuf
Protocol Buffers(简称protobuf)是Google开发的一种数据交换格式,它用于结构化数据的序列化。Protobuf是一种语言无关、平台无关、可扩展的序列化框架,类似于XML和JSON,但是它更小、更快、更简单。以下是Protobuf的一些关键特性:
- 定义数据结构:使用.proto文件定义数据结构,这是一种IDL(接口定义语言)文件,用于描述消息类型和数据结构。
- 语言无关性:Protobuf定义的数据结构可以被多种编程语言使用,包括但不限于C++、Java、Python、Go等。
- 高效序列化:Protobuf的序列化结果体积小,解析速度快,适合网络传输和存储。
- 向后兼容性:Protobuf支持向后兼容,可以在不破坏已有数据结构的前提下,添加或删除字段。
- 自动生成代码:使用Protobuf提供的工具,可以根据.proto文件自动生成各种语言的数据访问类代码,减少了手动编写和维护序列化代码的工作量。
- 版本控制:.proto文件可以被版本控制,方便跟踪数据结构的变更历史。
- 字段编码:Protobuf使用一种称为“tag”的机制为每个字段编号,这使得在解析消息时可以快速定位到特定的字段。
- 可选字段和默认值:Protobuf允许定义字段是否为必需的、可选的或重复的,并可以为字段设置默认值。
- 枚举和消息类型:Protobuf支持定义枚举类型和自定义消息类型,这使得数据结构更加清晰和易于管理。
- 服务定义:Protobuf还支持RPC(远程过程调用)服务的定义,可以用于构建分布式系统和微服务架构。
- 跨平台:Protobuf可以在不同的操作系统和硬件平台上使用,包括移动设备和嵌入式系统。
- 社区和工具支持:Protobuf有着广泛的社区支持,提供了大量的工具和库,方便开发者使用。
Protobuf被广泛应用于分布式系统、网络通信、数据存储等多个领域,特别是在需要跨语言和跨平台进行数据交换的场景中。它的设计目标是为了提高性能和效率,同时保持数据交换的灵活性和可扩展性。
Nested array of bytes
"Nested array of bytes"(嵌套字节数组)是一种数据结构,它在多个领域中被提及,尤其是在以太坊的上下文中。以下是关于nested array of bytes的介绍:
- 定义:Nested array of bytes是指一个由字节(byte)组成的数组,其中每个字节可以是0到255之间的整数。这种结构允许字节数组内部还可以包含其他字节数组,形成嵌套结构。
- 应用场景:在以太坊中,所有数据类型最终都会转换成nested array of bytes的形式。这是因为以太坊使用Recursive Length Prefix(RLP)编码,这是一种极简的序列化方法,它只支持两种数据类型:单个字节数组和字节数组的数组(即嵌套字节数组)。
- 序列化与反序列化:序列化是将数据结构或对象状态转换为可存储或可传输的格式(如字节流)的过程。反序列化则是将这种格式恢复为原始数据结构的过程。在以太坊中,RLP作为一种序列化机制,将复杂的数据结构转换为nested array of bytes,便于网络传输和存储。
- 以太坊中的使用:以太坊的状态树、交易树和收据树都使用RLP序列化来存储数据。状态树中保存的是key-value对,其中key是地址,value是账户状态,这些value通过RLP序列化后以nested array of bytes的形式存储。
- 数据结构的简化:RLP的设计理念是简单性,它只处理字符串(字节数组)和列表(嵌套递归的结构,可以包含字符串和列表)。这种简化使得RLP在实现上比一些更复杂的序列化库(如Protocol Buffers)更容易。
- 存储效率:使用nested array of bytes可以有效地利用存储空间,因为它允许数据以紧凑的二进制形式存在,这对于区块链这种需要高效存储解决方案的技术尤为重要。
- 跨语言和平台的兼容性:由于nested array of bytes基于基本的字节数据,它天然具有跨语言和平台的兼容性,这使得基于这种结构的数据可以在不同的系统和编程语言之间轻松传输和处理。
总的来说,nested array of bytes是一种灵活且高效的数据结构,它在以太坊中被广泛用于数据的序列化和存储,使得区块链数据可以以一种紧凑、有序且易于管理的方式存在。