算法之旅2.0-数据结构与算法
时间如白驹过隙,是时候来一趟算法之旅2.0了。
转眼就2023年了,去年大概了解了区块链、以太坊以及solidity。最近在看Go方面的内容,想着刚好就用Go再重走一遍来时路。顺便回顾一下多年以前,用Java过的一遍数据结构与算法,多年前的1.0版本还是比较简陋的。
不过确实工作中使用的比较少,平时业务开发不太需要复杂的数据结构,一般就是数组,列表,哈希表使用的最多,其他都在时间的长河中又还给大自然了。这次使用Go重来一次算法之旅,除了想温故知新外,主要也是熟练Go的基础,为了将来web3做准备,链上Solidity有了,再来一个链下的Go耍耍,毕竟大名鼎鼎的以太坊是用Go编写的。
接下来,开启2.0之旅吧。
算法无处不在
当我们听到“算法”这个词时,很自然地会想到数学。然而实际上,许多算法并不涉及复杂数学,而是更多地依赖基本逻辑,这些逻辑在我们的日常生活中处处可见。
在正式探讨算法之前,有一个有趣的事实值得分享:你已经在不知不觉中学会了许多算法,并习惯将它们应用到日常生活中了。下面我将举几个具体的例子来证实这一点。
例一:查字典
在字典里,每个汉字都对应一个拼音,而字典是按照拼音字母顺序排列的。假设我们需要查找一个拼音首字母为r的字。通常会按照如下方式实现。
- 1.翻开字典约一半的页数,查看该页的首字母是什么,假设首字母为m
- 2.由于在拼音字母表中r位于m之后,所以排除字典前半部分,查找范围缩小到后半部分。
- 3.不断重复步骤 1. 和步骤 2. ,直至找到拼音首字母为r的页码为止。
查字典这个小学生必备技能,实际上就是著名的二分查找算法。从数据结构的角度,我们可以把字典视为一个已排序的数组;从算法的角度,我们可以将上述查字典的一系列操作看作二分查找。
例二:整理扑克
在打牌时,每局都需要整理手中的扑克牌,使其从小到大排列,实现流程如图所示。
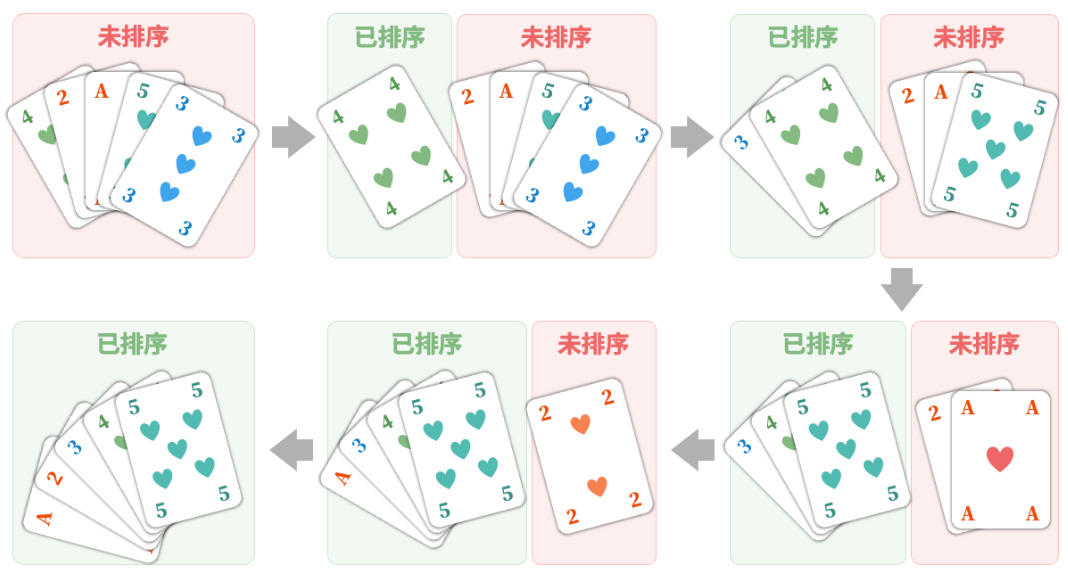
- 1.将扑克牌划分为“有序”和“无序”两部分,并假设初始状态下最左 1 张扑克牌已经有序。
- 2.在无序部分抽出一张扑克牌,插入至有序部分的正确位置;完成后最左 2 张扑克已经有序。
- 3.不断循环步骤 2. ,每一轮将一张扑克牌从无序部分插入至有序部分,直至所有扑克牌都有序。
上述整理扑克牌的方法本质上是插入排序算法,它在处理小型数据集时非常高效。许多编程语言的排序库函数中都有插入排序的身影。
例三:货币找零
假设我们在超市购买了69元的商品,给了收银员100元,则收银员需要找我们31元。他会很自然地完成如图所示的思考。
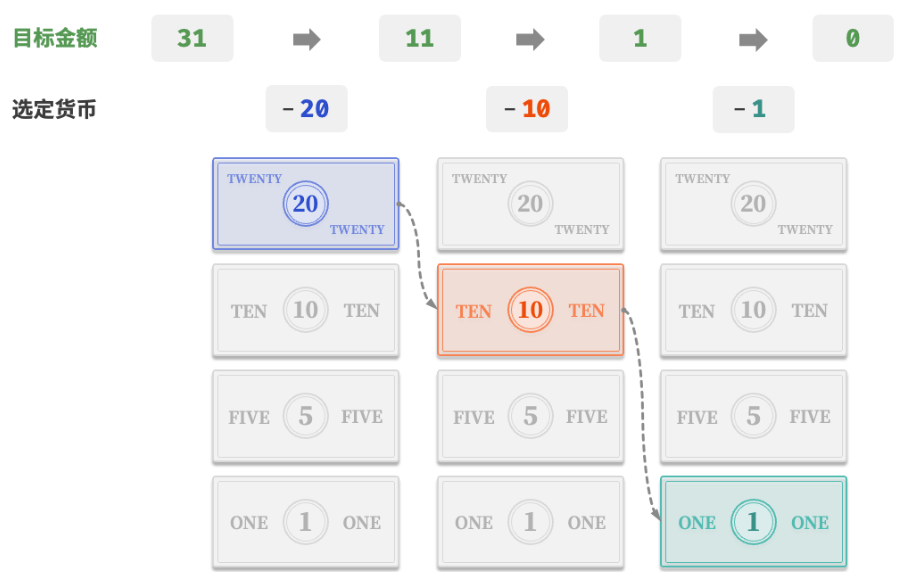
- 1.可选项是比31元面值更小的货币,包括1元,5元,10元,20元。
- 2.从可选项中拿出最大的20元,剩余31-20=11元。
- 3.从剩余可选项中拿出最大的10元,剩余11-10=1元。
- 4.从剩余可选项中拿出最大的1元,剩余1-1=0元。
- 5.完成找零,方案是20+10+1=31元。
在以上步骤中,我们每一步都采取当前看来最好的选择(尽可能用大面额的货币),最终得到了可行的找零方案。从数据结构与算法的角度看,这种方法本质上是贪心算法。
算法是什么
小到烹饪一道菜,大到星际航行,几乎所有问题的解决都离不开算法。计算机的出现使得我们能够通过编程将数据结构存储在内存中,同时编写代码调用 CPU 和 GPU 执行算法。这样一来,我们就能把生活中的问题转移到计算机上,以更高效的方式解决各种复杂问题。
算法定义
算法(algorithm)是在有限时间内解决特定问题的一组指令或操作步骤,它具有以下特性。
- 问题是明确的,包含清晰的输入和输出定义。
- 具有可行性,能够在有限步骤、时间和内存空间下完成。
- 各步骤都有确定的含义,在相同的输入和运行条件下,输出始终相同。
数据结构定义
数据结构(data structure)是组织和存储数据的方式,涵盖数据内容、数据之间关系和数据操作方法,它具有以下设计目标。
- 空间占用尽量少,以节省计算机内存。
- 数据操作尽可能快速,涵盖数据访问、添加、删除、更新等。
- 提供简洁的数据表示和逻辑信息,以便算法高效运行。
数据结构设计是一个充满权衡的过程。如果想在某方面取得提升,往往需要在另一方面作出妥协。下面举两个例子。
- 链表相较于数组,在数据添加和删除操作上更加便捷,但牺牲了数据访问速度。
- 图相较于链表,提供了更丰富的逻辑信息,但需要占用更大的内存空间。
数据结构与算法的关系
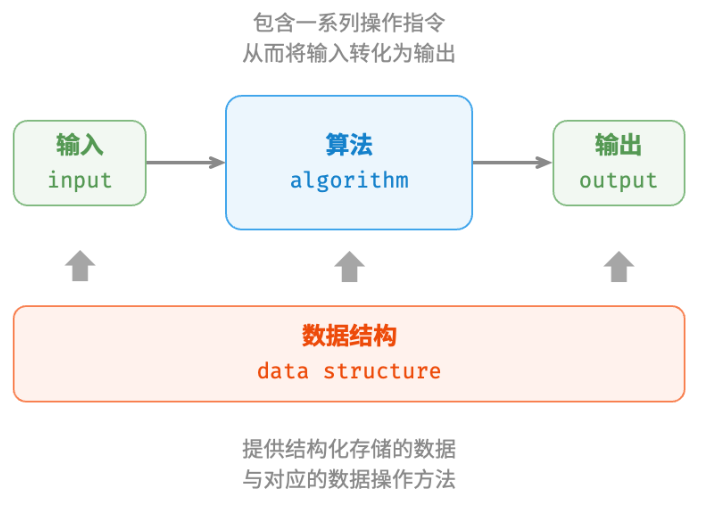
数据结构与算法高度相关、紧密结合,具体表现在以下三个方面。
- 数据结构是算法的基石。数据结构为算法提供了结构化存储的数据,以及操作数据的方法。
- 算法为数据结构注入生命力。数据结构本身仅存储数据信息,结合算法才能解决特定问题。
- 算法通常可以基于不同的数据结构实现,但执行效率可能相差很大,选择合适的数据结构是关键。
小结
回顾
- 算法在日常生活中无处不在,并不是遥不可及的高深知识。实际上,我们已经在不知不觉中学会了许多算法,用以解决生活中的大小问题。
- 查字典的原理与二分查找算法相一致。二分查找算法体现了分而治之的重要算法思想。
- 整理扑克的过程与插入排序算法非常类似。插入排序算法适合排序小型数据集。
- 货币找零的步骤本质上是贪心算法,每一步都采取当前看来最好的选择。
- 算法是在有限时间内解决特定问题的一组指令或操作步骤,而数据结构是计算机中组织和存储数据的方式。
- 数据结构与算法紧密相连。数据结构是算法的基石,而算法为数据结构注入生命力。
Q & A
算法(以及其他基础科目)的意义不是在于在工作中从零实现它,而是基于学到的知识,在解决问题时能够作出专业的反应和判断,从而提升工作的整体质量。
在工程领域中,大量问题是难以达到最优解的,许多问题只是被“差不多”地解决了。问题的难易程度一方面取决于问题本身的性质,另一方面也取决于观测问题的人的知识储备。人的知识越完备、经验越多,分析问题就会越深入,问题就能被解决得更优雅。