数据结构和算法之旅(六)- 堆
堆是一种基于树的数据结构,通常用完全二叉树实现。
在了解优先级队列中,接触过堆的概念,了解了堆的特性以及如何使用,这里看如何建立一个堆。
大顶堆
package org.example.datastructure;
import java.util.Arrays;
/**
* 大顶堆
* heapify建堆,使用弗洛伊德算符,时间复杂度O(n)
* 1.找到最后一个非叶子节点
* 2.从最后一个非叶子节点开始,依次下沉
* <p>
* heapify、down、up这是三个核心方法
*/
public class MaxHeap {
int[] array;
int size;
public MaxHeap(int[] array) {
this.array = array;
this.size = array.length;
heapify();
}
/**
* 建堆
*/
private void heapify() {
//如何找到最后一个非叶子节点 size/2-1
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
/**
* 删除堆顶元素
* 直接从索引0位置移除效率不高,所以先将它最后一个元素交换,
* 尾部移除,size-1就可以了,但可能导致不满足大顶堆特性,
* 需要做一次下潜
*/
public int poll() {
int top = array[0];
swap(0, size - 1);
size--;
down(0);
return top;
}
/**
* 删除指定索引处元素
*/
public int poll(int index) {
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
* 替换后可能不满足大顶堆特性,需要做一次下潜
*/
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
/**
* 获取堆顶元素
*/
public int peek() {
return array[0];
}
/**
* 向堆的尾部添加元素
*/
public boolean offer(int offered) {
if (size == array.length) {
return false;
}
up(offered);
size++;
return true;
}
/**
* 将inserted元素上浮:直至offered小于父元素或到堆顶
*/
private void up(int offered) {
int child = size;
while (child > 0) {
int parent = (child - 1) / 2;//父节点 公式
if (array[parent] >= offered)
array[child] = array[parent];
else
break;
child = parent;
}
array[child] = offered;
}
/**
* 将parent索引处元素下沉:与俩个孩子较大者交换,直至没孩子或孩子没它大
*/
public void down(int parent) {
int left = parent * 2 + 1;//左孩子 公式
int right = left + 1;//右孩子 公式
int max = parent;
if (left < size && array[left] > array[max]) max = left;
if (right < size && array[right] > array[max]) max = right;
if (max != parent) {//如果孩子比父亲大,就交换
swap(max, parent);
down(max);//递归
}
}
/**
* 交换俩个索引处元素
*/
public void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
//test
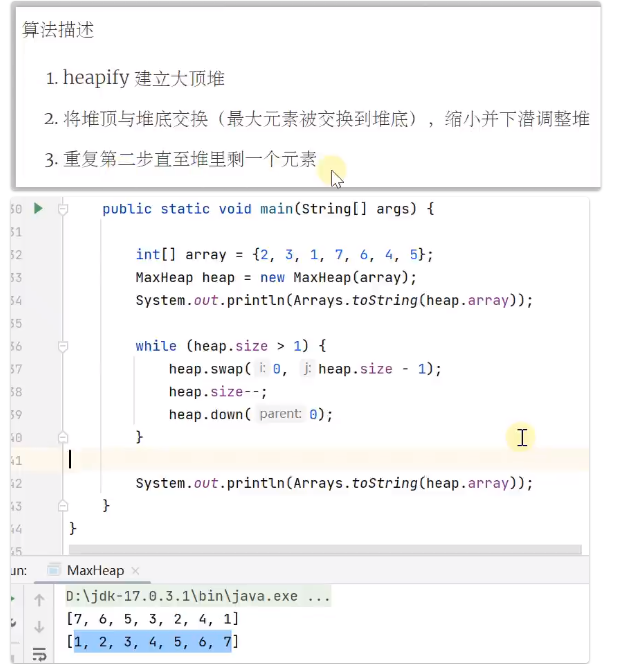
public static void main(String[] args) {
int[] array = {1, 2, 3, 4, 5, 6, 7};
MaxHeap maxHeap = new MaxHeap(array);
System.out.println(Arrays.toString(maxHeap.array));
}
}堆排序