数据结构和算法之旅(三)- 递归
在计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集。
定义
比如,单链表递归遍历的例子。
void f(Node node){
f(node.next);
}
说明:
1.自己调用自己,如果每个函数对应着一种解决方案,自己调用自己意味着解决方案是一样的(有规律的)
2.每次调用,函数处理的数据会比上次缩减(子集),而且最后会缩减至无需继续递归。
3.内存函数调用(子集处理)完成,外层函数才能算调用完成!
单链表递归分析


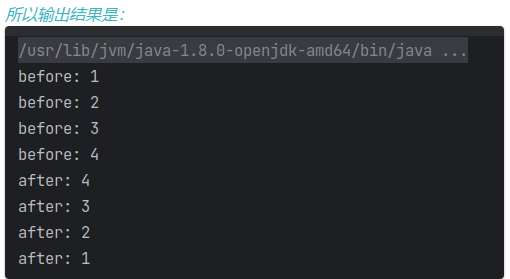
递归思路

深入到最里面叫做递。
从最里面出来叫做归。
在递的过程中,外层函数的局部变量以及方法参数并未消失,归的时候还可以使用。
阶乘
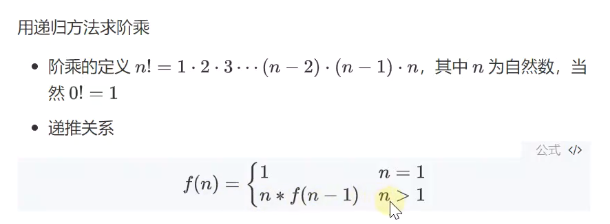
private static int f(int n){
if(n == 1)
return 1;
return n * f(n-1);
}伪代码,分析执行流程如下:
f(int n = 3){
return 3 * f(int n = 2){
return 2 * f(int n = 1){
if(n == 1){
return 1;
}
}
}反向打印字符串

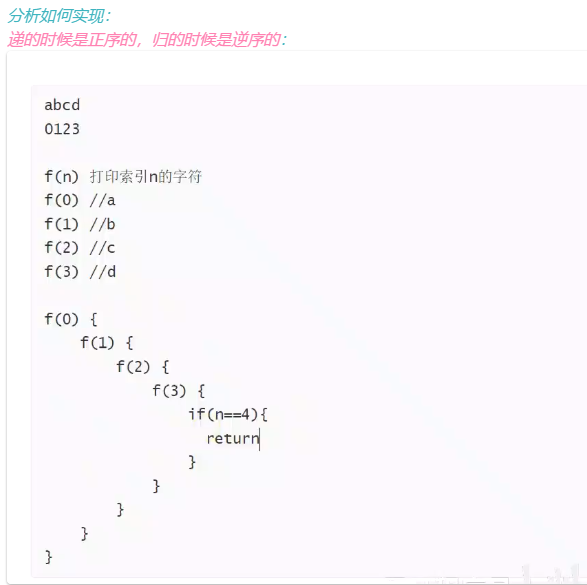
/*
因为递的时候是正序的,归的时候逆序的,所以把递归调用放在前面,打印放在后面,即可实现
*/
public class ReversePrintString{
public static void f(int n, String str){
if(n == str.length()) return;
f(n + 1, str);//递
System.out.println(str.charAt(n));
}
}二分查找
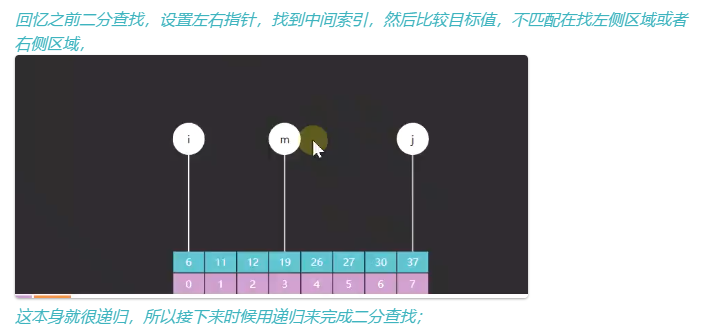
/*
递归实现二分查找
*/
public class RecursionBinarySearch{
public static void main(String[] args){
int[] a = {7,13,21,30,38,44,52,53};
System.out.println(search(a, 7)); //0
System.out.println(search(a, 13));//1
System.out.println(search(a, 21));//2
System.out.println(search(a, 53));//7
}
public static int search(int[] a, int target){
//让调用者少传参数, 隐藏具体实现
return f(a, target, 0, a.length - 1);
}
/**
* left和right不对外暴露,让调用者使用更简单
* 返回目标索引
* 找不到返回-1
*/
priavte static int f(int[] a, int target, int left, int right){
if(left > right) return -1; //递归终止条件
int m = (left + right) >>> 1;
if(target < a[m]){
return f(a, target, left, m - 1);
}else if(a[m] < target){
return f(a, targetm m + 1, right);
}else{
return m;
}
}
}冒泡排序0(n^2)
以下是冒泡排序的实现原理步骤:
- 从列表的第一个元素开始,比较它与下一个元素的大小。
- 如果第一个元素大于第二个元素(逆序),则交换它们的位置。
- 移动到下一个元素,重复步骤1和步骤2,直到列表的末尾。
- 重复上述步骤,每次内部循环将最大的元素 "冒泡" 到列表的最后一个位置。
- 外部循环减小待排序元素的范围,直到没有需要交换的元素为止,表示排序完成。
冒泡排序的特点是每一轮内部循环都将当前未排序部分中的最大元素移动到了最后。这意味着在每一轮后,最后的元素都会是当前未排序部分的最大值。排序过程中,如果一轮内部循环没有发生任何交换,就可以提前结束排序,因为列表已经是有序的。
用递归实现冒泡过程分析:
1.将数组划分成俩部分 [0..j],[j+1 .. a.length-1]。
2.左边[0..j] 是未排序的部分。
3.右边[j+1 .. a.length-1]是已排序部分。
4.未排序区间内,相邻俩个元素比较,如果前一个大,则交换位置。
public class BubbleSort{
public static void sort(int[] a){
bubble(a, a.length-1);
}
//j 代表未排序区域的右边界
//bubble内部首先是递归结束条件,然后for循环是一次冒泡,然后调用自身
private static void bubble(int[] a, int j){
if(j == 0){
return;
}
for(int i = 0; i < j; i++){
if(a[i] > a[i+1]){
int t = a[i];
a[i] = a[i+1];
a[i+1] = t;
}
}
bubble(a, j-1);
}
}优化
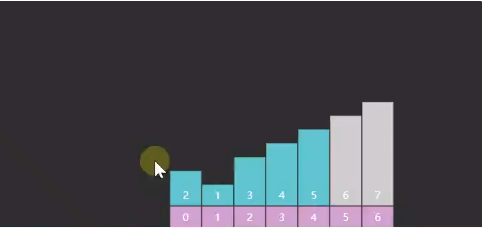
这种情况下,未排序区域还很大,但是只需要在冒泡一次,把2和1交换就达到目的了,但是未排序边界 j 还没有到 0 ,会做很多无用功。尝试优化一下。
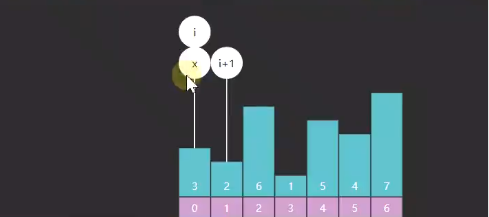
可以搞一个 x ,初始为0,如果当次产生交换,就让所以 i 的索引赋给 x,如果没有产生交换,x 就保持上一次的不变,那么 x 就能当做无序和有序的边界了,下次递归就不用 j 去递减了。
public class BubbleSort{
public static void sort(int[] a){
bubble(a, a.length-1);
}
//j 代表未排序区域的右边界
//bubble内部首先是递归结束条件,然后for循环是一次冒泡,然后调用自身
private static void bubble(int[] a, int j){
if(j == 0){
return;
}
int x = 0;
for(int i = 0; i < j; i++){
if(a[i] > a[i+1]){
int t = a[i];
a[i] = a[i+1];
a[i+1] = t;
x = i;
}
}
bubble(a, x);
}
}插入排序O(n^2)
它的工作方式优点像整理一手扑克牌,以下是插入排序的实现原理步骤:
- 从第二个元素开始(索引为1),将当前元素视为待插入的元素。
- 将待插入的元素与已排序部分的元素逐个比较,直到找到一个比待插入元素小的元素,或者已经遍历完已排序部分。
- 将待插入元素插入到找到的位置,使得已排序部分仍然保持有序。
- 重复上述步骤,逐个处理未排序部分的元素,直到整个列表都有序。
插入排序的特点是在每一轮内部循环中,将当前未排序元素插入到已排序部分的合适位置,逐步扩展已排序部分。这使得已排序部分始终保持有序。插入排序适用于小型数据集或基本有序的数据集,因为它的时间复杂度为 O(n^2),在大型数据集上性能较差。
public static void sort(int[] a){
insertion(a, 1);
}
/*
用递归实现
low是未排序的左边界,从1开始
*/
private static void insertion(int[] a, int low){
if(low == a.length){
return;
}
int t = a[low];
int i = low - 1;//已排序区域指针
while(i>=0 && a[i]>t){//没有找到插入位置
a[i+1] = a[i];//空出插入位置
i--;
}
//找到插入位置
a[i+1] = t;
insertion(a, low+1);
}斐波那契数列(多路递归)

public class Fibonacci{
public static int f(int n){
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
int x = f(n - 1);
int y = f(n - 2);
return x + y;
}
}斐波那契是多路递归的典型案例,整个计算过程相当于二叉树了,其中很多重复的步骤,造成时间复杂度很差。
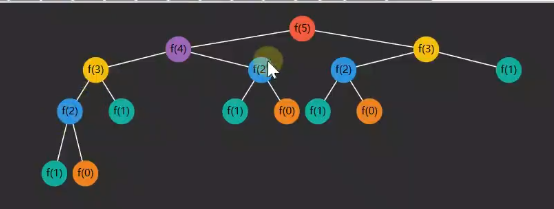
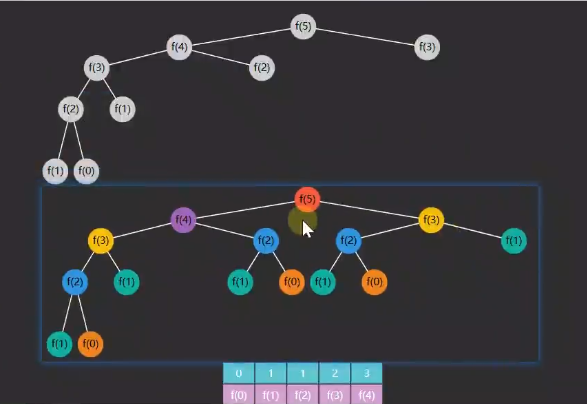
可以看出,上面计算过程有很多重复,可以定义一个数组,存储 f(n) 的解,将来计算到哪一项的时候,如果数组有就直接从数组取,可以大大优化;
这种方式称为记忆法,也称为备忘录,其实就是剪枝的过程。
改进之后时间复杂度从O(1.68n)优化为O(n)。但因额外产生数组,这就是空间换时间。
public static int fbonacci(int n){
int[] cache = new int[n + 1];
Arrays.fill(cache, -1);//都填充-1
cache[0] = 0;
cache[1] = 1;
return f(n, cache);
}
public static int f(int n, int[] cache){
if(cache[n] != -1){
return cache[n];
}
int x = f(n-1, cache);
int y = f(n-2, cache);
cache[n] = x + y;//存入数组
return cache[n];
}递归求和
public class Sum{
//f(n) = f(n-1) + n;
public static long sum(long n){
if(n == 1){
return 1;
}
return sum(n-1) + n;
}
}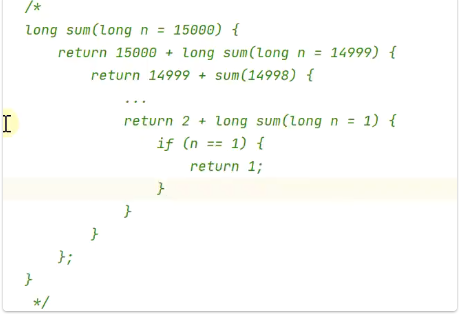
递归求和,属于单路递归,很容易就想到了思路,为什么贴上这个呢。可以把n等于15000试一下,就很发现为什么了。因为栈内存溢出了!也就是爆栈了!
只有最内层的sum(n = 1)的函数执行完了,才能一层一层往外归。也就是说递的过程必须递到最深处才能归!!!每个方法调用是需要消耗内存的,需要存储方法的相关信息,比如说方法的参数信息,方法内的局部变量,方法的返回地址,这些信息都需要存放在栈内存中,在最内层n = 1没有结束之前,前面14999个方法都需要等着!!它们占用的内存也不能得到释放。所以会导致占内存溢出。
尾调用&尾递归
在解决爆栈问题之前,需要掌握几个其他知识。
尾调用:如果函数的最后一步是调用一个函数,称为尾调用。
尾递归:在函数内部最后调用自己,称为尾递归。
能对尾递归优化的语言有c++、scala,它们会把逐级递归的方式改成平级的形式。scala也属于java的近亲,也是编译成class类在JVM上运行,有幸了解过一些。
当然,从根本上避免爆栈问题,就是避免使用递归。把递归代码改成循环代码。理论上所有递归都能改写成循环代码。
经典白学,哈哈哈哈