数据结构和算法之旅(九)- AVL树
通过旋转操作保持树的平衡,确保查找、插入和删除操作的时间复杂度都是O(log n),适用于高效的数据组织和搜索。
二叉搜索树,如果不平衡,那么查找效率就会从对数级降级成O(n)。
可以通过旋转来恢复平衡,而且旋转并不影响二叉搜索树的特性。
那么,如何判断是否不平衡呢,是有个结论的:
如果一个节点的左右孩子,高度差超过1,则此节点失衡,才需要旋转。
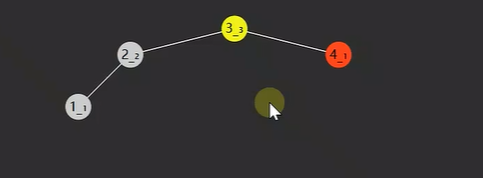
定义
- 二叉搜索树在插入和删除时,节点可能失衡。
- 如果在插入和删除时通过旋转,始终让二叉搜索树保持平衡,称为自平衡的二叉搜索树。
- AVL是自平衡二叉搜索树的实现之一。
旋转分析
失衡有四种情况LL、LR、RL、RR,但基本的选择操作有俩种就是左旋或右旋。
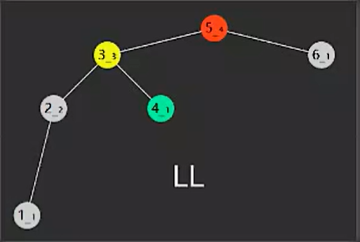
LL
- 失衡节点(图中5红色)的bf > 1,即左边更高
- 失衡节点的左孩子(图中3黄色)的bf >= 0,即左孩子也是左边更高或等高
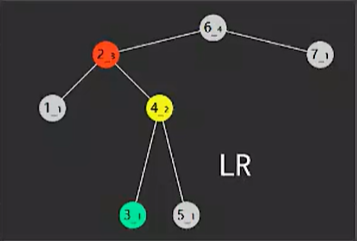
LR
- 失衡节点(图中6)的bf > 1,即左边高
- 失衡节点的左孩子(图中2红色)的bf < 0,即左孩子是右边高
RL
- 失衡节点(图中2)的bf < -1 ,即右边高
- 失衡节点的右孩子(图中6红色)的bf > 0 ,即右孩子的左边更高
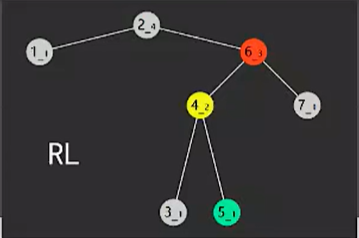
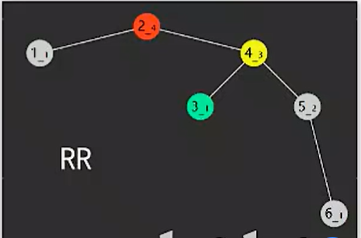
RR
- 失衡节点(图中2红色)的bf < -1 ,即右边更高
- 失衡节点(图中6黄色)的bf <= 0,即右孩子的右边更高或等高
code
package avl;
public class AVLTree {
AVLNode root;
static class AVLNode {
int key;
Object value;
AVLNode left;
AVLNode right;
int height = 1;//高度
public AVLNode(int key, Object value) {
this.key = key;
this.value = value;
}
public AVLNode(int key) {
this.key = key;
}
public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
//求节点的高度
private int height(AVLNode node) {
return node == null ? 0 : node.height;
}
//更新节点高度(新增、删除、旋转)
private void updateHeight(AVLNode node) {
//就是找左或右深度加1
node.height = Integer.max(height(node.left), height(node.right)) + 1;
}
/**
* 平衡因子balance factor = 左子树高度-右子树高度
* 0 , -1, 1 都是平衡的
* bf>1,不平衡,表示左边高
* bf<-1,不平衡,表示右边高
*/
private int bf(AVLNode node) {
return height(node.left) - height(node.right);
}
/**
* 右旋,就是把根旋转下去,把左子树旋转上来
*
* @param node 要旋转的节点
* @return 选装上去的新的根节点
*/
private AVLNode rightRotate(AVLNode node) {
AVLNode left = node.left;//找到左子树
left.right = node;//顶上去
node.left = left.right;//换爹的
updateHeight(node);//更新高度
updateHeight(left);//更新高度
return left;
}
/**
* 左旋,就是把根旋转下去,把右子树旋转上来
*
* @param node 要旋转的节点
* @return 选装上去的新的根节点
*/
private AVLNode leftRotate(AVLNode node) {
AVLNode right = node.right;//找到右子树
right.left = node;//顶上去
node.right = right.left;//换爹的
updateHeight(node);//更新高度
updateHeight(right);//更新高度
return right;
}
//先左旋左子树,再右旋根节点
private AVLNode leftRightRotate(AVLNode node) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
//先右旋右子树,在左旋根节点
private AVLNode rightLeftRotate(AVLNode node) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
/**
* 检查节点是否失衡,重新平衡
*/
private AVLNode balance(AVLNode node) {
if (node == null) return null;
int bf = bf(node);
if (bf > 1 && bf(node.left) >= 0) {//LL 考虑删除引发的不平衡,加个等号
return leftRotate(node);
} else if (bf > 1 && bf(node.left) < 0) {//LR
return leftRightRotate(node);
} else if (bf < -1 && bf(node.right) > 0) {//RL
return rightLeftRotate(node);
} else if (bf < -1 && bf(node.right) <= 0) {//RR 考虑删除引发的不平衡,加个等号
return rightRotate(node);
}
return node;
}
/**
* 新增&更新
*/
public void put(int key, Object value) {
root = doPut(root, key, value);
}
/**
* 递归实现put
*/ private AVLNode doPut(AVLNode node, int key, Object value) {
//1.找到空位,创建新节点
if (node == null) {
return new AVLNode(key, value);
}
//2.key已存在,更新
if (key == node.key) {
node.value = value;
return node;
}
//3.继续查找
if (key < node.key) {
node.left = doPut(node.left, key, value);
} else {
node.right = doPut(node.right, key, value);
}
updateHeight(node);
return balance(node);
}
/**
* 删除
*/
public void remove() {
root = doRemove(root, root.key);
}
private AVLNode doRemove(AVLNode node, int key) {
//1.node==null
if (node == null) return null;
//2.没找到key继续递归
if (key < node.key) {
node.left = doRemove(node.left, key);
} else if (node.key < key) {
node.right = doRemove(node.right, key);
} else {
//3.找到key 1.没有孩子 2.只有一个孩子 3有俩个孩子
if (node.left == null && node.right == null) {
return null;
} else if (node.left == null) {
node = node.right;//暂存给node 等待更新高度和平衡
} else if (node.right == null) {
node = node.left;//暂存给node 等待更新高度和平衡
} else {
//找后续:右子树的最左
//处理后事
//顶替
AVLNode s = node.right;
while (s.left != null) {
s = s.left;
}
s.right = doRemove(node.right, s.key);
s.left = node.left;
node = s;
}
}
//4.更新高度
updateHeight(node);
//5.balance
return balance(node);
}
}