数据结构和算法之旅(十)- 红黑树
红黑树也是一种自平衡的二叉搜索树,较之AVL,插入和删除旋转次数更少。性能上要稍微高一些。
定义
红黑树特性:
- 1.所有节点都有俩种颜色:红与黑
- 2.所有null视为黑色
- 3.红色节点不能相邻,(判断平衡的主要依据)
- 4.根节点时黑色
- 5.从根到任意一个叶子节点,路径中的黑色节点数一样(判断平衡的主要依据)
不满足这些特性的都是不平衡的红黑树。
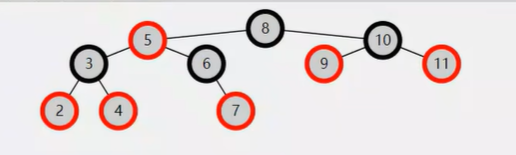
是否是红黑树?
树1
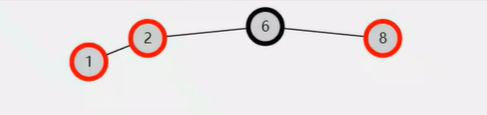
不是红黑树。 因为违反了第3条:红色节点不能相邻。
树2
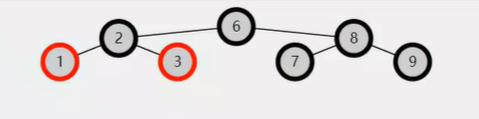
不是红黑树。 因为违反了第5条:从根到任意一个叶子节点,路径中黑色节点数一样。 右边重,左边轻,是不平衡的。
树3
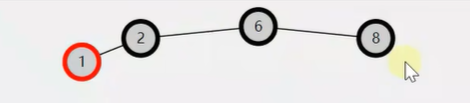
是红黑树。 关键的3,4,5条特性都满足。
树4
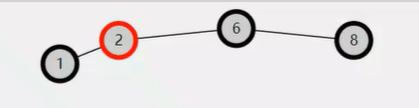
这个和上一个类似,但是它并不是平衡的。
因为没有考虑null值。
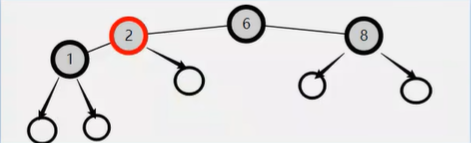
那什么时候需要考虑null呢,就是当叶子节点没有自己的兄弟的时候,这个时候就需要把null加进来考虑。
如果加入null值,如下图, 6到2的右孩子只有俩个黑色,而6到1或者8的孩子都是3个黑色,所以是不平衡的。
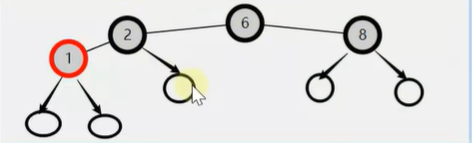
那为什么树3是平衡的红黑树呢?可以把null考虑进来,可以看出根到任意叶子节点的黑色数都是3,所以是平衡的。
判断是否平衡有一点经验总结。
如果叶子节点是红色,可以不用不用care。
如果叶子节点就一个黑色,没有兄弟节点,那肯定是不平衡的。
红色节点无所谓,黑色节点肯定要成对出现的。
code
package redblack;
import com.sun.org.apache.regexp.internal.RE;
public class RedBlackTree {
enum Color {
RED, BLACK;
}
private Node root;
private static class Node {
int key;
Object value;
Node left;
Node right;
Node parent;//父节点 因为红黑树的删除和新增经常用到父节点
Color color = Color.RED;//默认刚创建出来新节点是为红色
public Node(int key, Object value) {
this.key = key;
this.value = value;
}
//是否是左孩子 常用工具方法
boolean isLeftChild() {
//如果父节点不为空且父节点的left是自身则是左孩子
return parent != null && parent.left == this;
}
//叔叔 常用工具方法
Node uncle() {
if (parent == null || parent.parent == null) {
return null;//没有爷爷就没有叔叔
}
if (parent.isLeftChild()) {
return parent.parent.right;
} else {
return parent.parent.left;
}
}
//兄弟 常用工具方法
Node sibling() {
if (parent == null) {
return null;//没父亲就没兄弟
}
if (this.isLeftChild()) {
return parent.right;
} else {
return parent.left;
}
}
}
//判断红、黑
boolean isRed(Node node) {
return node != null && node.color == Color.RED;
}
boolean isBlack(Node node) {
return node == null || node.color == Color.BLACK;
}
//右选 1.parent的处理 2.旋转后新根的父子关系
private void rightRotate(Node pink) {
Node parent = pink.parent;//pink不平衡的节点
Node yellow = pink.left;//yellow新根
Node green = yellow.right;//green要换爹的
if (green != null) {
green.parent = pink;
}
yellow.right = pink;//顶上去
yellow.parent = parent;
pink.left = green;
pink.parent = yellow;
if (parent == null) {
root = yellow;
} else if (parent.left == pink) {
parent.left = yellow;
} else {
parent.right = yellow;
}
}
//左旋
private void leftRotate(Node pink) {
Node parent = pink.parent;//pink不平衡的节点
Node yellow = pink.right;//yellow新根
Node green = yellow.left;//green要换爹的
if (green != null) {
green.parent = pink;
}
yellow.left = pink;//顶上去
yellow.parent = parent;
pink.right = green;
pink.parent = yellow;
if (parent == null) {
root = yellow;
} else if (parent.right == pink) {
parent.right = yellow;
} else {
parent.left = yellow;
}
}
/**
* 新增或更新
* 找空位,找到之后根据k-v创建新的节点对象,然后根父节点建立好父子关系,新增操作就算完成了。
* 如果没有找到空位,就根据key的大小不断的向左找向右找。
* 如果找相同的key,就是更新。
* <p>
* 正常增,遇到红红不平衡进行调整
* 红红不平衡细分有四种case。
*/
public void put(int key, Object value) {
Node p = root;
Node parent = null;//记录新增节点的父节点
while (p != null) {
parent = p;
if (key < p.key) {
p = p.left;
} else if (p.key < key) {
p = p.right;
} else {
p.value = value;//更新
return;
}
}
Node inserted = new Node(key, value);
if (parent == null) root = inserted;
else if (key < parent.key) {
parent.left = inserted;
inserted.parent = parent;//1.维护parent属性
} else {
parent.right = inserted;
inserted.parent = parent;//1.维护parent属性
}
fixRedRed(inserted);
}
//修复红红
void fixRedRed(Node x) {
//case 1.插入节点是根节点,变黑集合
if (x == root) {
x.color = Color.BLACK;
return;
}
//case 2.插入节点父亲是黑色,无需调整
if (isBlack(x.parent)) {
return;
}
/*
case 3.当红红相邻,叔叔为红色时
需要将父亲、叔叔变黑、祖父变红,然后对祖父做递归处理
*/ Node parent = x.parent;
Node uncle = x.uncle();
Node grandparent = parent.parent;
if (isRed(uncle)) {
parent.color = Color.BLACK;
uncle.color = Color.BLACK;
grandparent.color = Color.RED;
fixRedRed(grandparent);
}
//case 4.
if (parent.isLeftChild() && x.isLeftChild()) {//LL
parent.color = Color.BLACK;
grandparent.color = Color.RED;
rightRotate(grandparent);
} else if (parent.isLeftChild() && !x.isLeftChild()) {//RL
leftRotate(parent);//使之变成LL case
x.color = Color.BLACK;
grandparent.color = Color.RED;
rightRotate(grandparent);
} else if (!parent.isLeftChild() && !x.isLeftChild()) {//RR
parent.color = Color.BLACK;
grandparent.color = Color.RED;
leftRotate(grandparent);
} else {//LR
rightRotate(parent);////使之变成RR case
x.color = Color.BLACK;
grandparent.color = Color.RED;
leftRotate(grandparent);
}
}
/**
* 查找删除节点
*/
private Node find(int key) {
Node p = root;
while (p != null) {
if (key < p.key) {
p = p.left;
} else if (p.key < key) {
p = p.right;
} else {
return p;
}
}
return null;
}
/**
* 查找剩余节点
*/
private Node findReplaced(Node deleted) {
if (deleted.left == null && deleted.right == null) {
return null;
}
if (deleted.left == null) {
return deleted.right;
}
if (deleted.right == null) {
return deleted.left;
}
//有俩个孩子,要找后继节点(右子树的最左)
Node s = deleted.right;
while (s.left != null) {
s = s.left;
}
return s;
}
/**
* 删除
* 正常删、会用到李代桃僵的技巧,遇到黑黑不平衡进行调整
* 黑黑不平衡细分有6种case。
*/
public void remove(int key) {
Node deleted = find(key);
if (deleted == null) return;
doRemove(deleted);
}
private void doRemove(Node deleted) {
Node replaced = findReplaced(deleted);
Node parent = deleted.parent;
if (replaced == null) {//没有孩子
//case 1.删的根节点
if (deleted == root) {
root = null;
} else {
if (isBlack(deleted)) {//删除到节点时黑,剩余的也是黑,双黑(null也是黑)
//复杂调整
fixDoubleBlack(deleted);//先调整平衡,下面在删除
} else {
//红色叶子,无需任何处理
}
//case 2.不是根节点 并没有孩子
if (deleted.isLeftChild()) {
parent.left = null;
} else {
parent.right = null;
}
deleted.parent = null;//help GC
}
return;
}
if (deleted.left == null || deleted.right == null) {//有一个孩子
if (deleted == root) {
//case 1.删的根节点
root.key = replaced.key;
root.value = replaced.value;
root.left = root.right = null;
} else {
//case 2.不是根节点 并有一个孩子
if (deleted.isLeftChild()) {
parent.left = replaced;
} else {
parent.right = replaced;
}
replaced.parent = parent;
deleted.left = deleted.right = deleted.parent = null;//help GC
if (isBlack(deleted) && isBlack(replaced)) {//删除到节点时黑,剩余的也是黑,双黑
//复杂调整
fixDoubleBlack(replaced);//上面先删除了,再调整
} else {
//case 2
replaced.color = Color.BLACK;
}
}
return;
}
//有俩个孩子,找到后继,替换,删除后继节点
int t = deleted.key;
deleted.key = replaced.key;
replaced.key = t;
Object v = deleted.value;
deleted.value = replaced.value;
replaced.value = v;
doRemove(replaced);
}
/**
* 处理双黑
* 删除到节点和剩下的节点都是黑,触发双黑,双黑的意思是,整个路径上少一个黑!需要调整
* case 3:被调整节点的兄弟为红,此时俩个侄子定为黑(过度情况,需要转换成4或5,通过旋转)
* case 4:被调整节点的兄弟为黑,俩个侄子都为黑
* case 5:被调整节点的兄弟为黑,至少一个红侄子
*/
private void fixDoubleBlack(Node x) {
if (x == root) {//递归结束条件
return;
}
Node parent = x.parent;//父
Node sibling = x.sibling();//兄弟
//case 3:兄弟节点是红色
if (isRed(sibling)) {
if (x.isLeftChild()) {//旋转
leftRotate(parent);
} else {
rightRotate(parent);
}
parent.color = Color.RED;//换色
sibling.color = Color.BLACK;
fixDoubleBlack(x);
return;
}
//case 4:兄弟节点是黑色,俩个侄子都是黑
if (sibling != null) {
if (isBlack(sibling.left) && isBlack(sibling.right)) {
sibling.color = Color.RED;
if (isRed(parent)) {
parent.color = Color.BLACK;
} else {
fixDoubleBlack(parent);
}
} else {
//case 5:兄弟是黑色,但是侄子有红色
//LL 兄弟是左孩子,左侄子是红
if (sibling.isLeftChild() && isRed(sibling.left)) {
rightRotate(parent);
sibling.left.color = Color.BLACK;
sibling.color = parent.color;
}
//LR 兄弟是左孩子,右侄子是红
else if (sibling.isLeftChild() && isRed(sibling.right)) {
sibling.right.color = parent.color;
leftRotate(sibling);
rightRotate(parent);
}
//RR 兄弟是右孩子,右侄子是红
else if (!sibling.isLeftChild() && isRed(sibling.left)) {
sibling.left.color = parent.color;
rightRotate(sibling);
leftRotate(parent);
}
//RL 兄弟是右孩子,左侄子是红
else {
leftRotate(parent);
sibling.right.color = Color.BLACK;
sibling.color = parent.color;
}
parent.color = Color.BLACK;
}
} else {
fixDoubleBlack(parent);
}
}
}右旋
旋转前
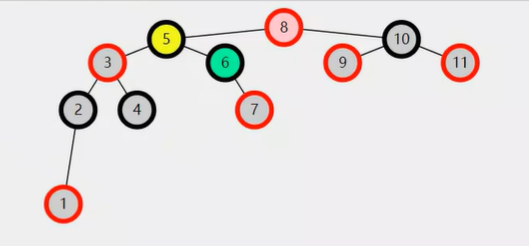
旋转后
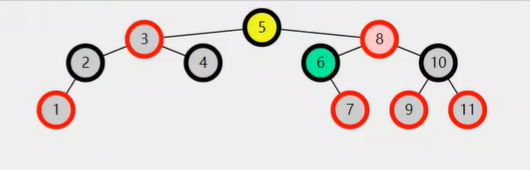
理解旋转,对照图,标记颜色有助于帮助理解,和代码实现。
📌旋转前: yellow是pink的左孩子;Node yellow = pink.left green是yellow的右孩子;Node green = yellow.right 📌旋转后: yellow要顶上去,成为新根; pink要下去,成为yellow的右孩子;yellow.right = pink 而且pink的左孩子变成了green; pink.left = green
到这一步,如果是AVL树就完事了,不过红黑树还要维护一个parent,🙃 还需要继续处理,并且要把新根yellow的父子关系直接在旋转这个方法里给搭建好;
接下来就把pink、yellow、green的parent属性处理好。
1️⃣ 处理green的parent: 旋转前,green的parent是yellow; 旋转后,green的parent是pink; 所以green的parent要重新赋值,当然green并不一定存在,所以需要一个判断: if(green != null) green.parent = pink;
2️⃣ 处理yellow的parent: 旋转前,yellow的parent是pink; 旋转后,yellow成了pink的parent; 该图列不存在5,8的parent,但是可能存在,所以, yellow.parent = pink.parent 等价于 yellow.parent = parent, 因为这个parent就是通过Node parent = pink.parent拿到的。
3️⃣ 处理pink的parent: 旋转后,pink的parent变成了yellow; 所以pink.parent = yellow
还有一件事,就是处理好新根的父子关系,该图例有些特殊,直接就是根了,看一下下面图例:
旋转前
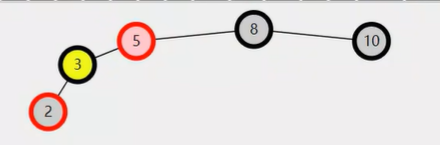
旋转后
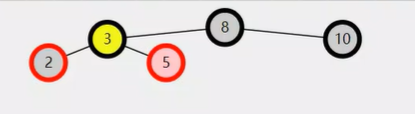
要维护yellow顶上去之后的parent父子关系。 旋转前,通过Node parent = pink.parent; 拿到之前的根。 旋转后,需要判断之前pink是它的父的左还是右孩子,就可以判断之后,决定yellow是之前根到左还是右,所以:
if(parent.left == pink){
parent.left = yellow;
}else{
parent.right = yellow;
}最后再考虑之前的特殊情况, 
pink是之前的根,它的parent是null,那去给它的left、right赋值肯定是有问题的,所以应该排除这种情况,直接把yellow作为root即可:
if(parent == null) root = yellow;
else if(parent.left == pink){//把上面的非根情况逻辑补充上
parent.left = yellow;
}else{
parent.right = yellow;
}左旋
其实左旋类似右旋,只不过反过来。可以通过着色法搞一下,比对右旋加深理解。
新增或更新
新增的时候,跟基本的二叉搜索树一致,只不过多两件事
- 1.要维护新增节点的parent属性
- 2.要维护红红的不平衡,因为新增的是默认红色
红红不平衡,细分有四种case: 因为插入节点均视为红色🔴
- case 1.插入节点为根节点,将根节点变黑⚫️
- case 2.插入节点的父节点若为黑色⚫️,树的红黑性质不变,无序调整 插入节点的父节点为红色🔴,触发红红相邻
- case 3.叔叔为红色🔴
- 1.父亲变为黑色⚫️,为了保证黑色平衡,连带叔叔也变成黑色⚫️
- 2.祖父如果是黑色不变,会造成这个子树黑色过多,因此祖父也变为红色🔴
- 3.祖父如果变成红色,可能会接着触发红红相邻,因此继续对祖父进行递归调整
- 4.直到根节点,如果root变为红色,改为红色就完成了
- case 4.叔叔为黑色⚫️
- 1.父亲为左孩子,插入节点也是左孩子,此时即LL不平衡
- 2.父亲为左孩子,插入节点是右孩子,此时即LR不平衡
- 3.父亲为右孩子,插入节点也是右孩子,此时即RR不平衡
- 4.父亲为右孩子,插入节点是左孩子,此时即RL不平衡
删除
删除可能触发双黑的情况,触发双黑,双黑的意思是,整个路径上少一个黑!需要调整也有很多case如下:
- case 0:如果删除节点有俩个孩子,化简成只有一个孩子或没有孩子(替换删除)
- csae 1:删除到是根节点
- case 2:删除的是黑⚫️,剩下的红🔴,剩下这个红节点变黑⚫️
- case 3:被调整节点的兄弟为红🔴,此时俩个侄子定为黑⚫️
- case 4:被调整节点的兄弟是黑⚫️,俩个侄子都为黑⚫️
- case 5:被调整节点的兄弟是黑⚫️,至少一个红🔴侄子
- 如果兄弟是左孩子,左侄子是红🔴,LL不平衡
- 如果兄弟是左孩子,右侄子是红🔴,LR不平衡
- 如果兄弟是右孩子,右侄子是红🔴,RR不平衡
- 如果兄弟是右孩子,左侄子是红🔴,RL不平衡