数据结构和算法之旅(零)- 认识算法
从今天开始,重新认识一下算法。
通过二分查找算法,认识算法。 需求:在有序数组A内,查找值target: 1.如果找到返回索引; 2.如果找不到返回-1;
二分查找算法
分析
根据需求,可以直观的想出来的解法如下:
- 前提:给定一个内含n个元素的有序数组A,查找指定值target;
- 1.设置
i = 0为左边界索引,j = n - 1为右边界索引; - 2.如果
i > j,结束查找,没找到; - 3.设置
m = medium((i+j)/2),m为中间索引,medium是向下取整的最小整数; - 4.如果
target < A[m],设置j = m - 1,转第二步; - 5.如果
A[m] < target,设置i = m + 1,转第二步; - 6.如果
A[m] = target,结束查找,说明找到了;
code
public static int binarySearchBasic(int[] a, int target){
int i = 0, j = a.length - 1;//设置指针和初值
while(i<=j){
//int m = (i+j)/2;//java除法自动取整,但除法有隐患,当然数值范围不大可以忽略
int m = (i+j)>>>1;//无符号右移,相当于除以2,且能避免隐患
if(target<a[m]){
//如果目标在中间值的左边,设置右边界指针为中间索引-1
j = m - 1;
}else if(a[m]<target){
//如果目标在中间值的右边,设置左边界指针为中间索引+1
i = m + 1;
}else{
//找到了
return m;
}
}
return -1;
}why
Q:为什么是i <= j 意味着区间内有未比较的元素,而不是i < j ?
A:因为i=j 指向的元素也有可能是要查找的目标,如果没有等号,就会漏掉一次比较;
Q:(i+j)/2 有没有问题?为什么使用右移代替?
A:因为如果数组无限大,j初始是Integer.MAX_VALUE - 1。第一次(i+j)/2没问题,但是如果此时,目标值比中间值大,需要把左侧i边界设置为m+1,那么此时,再进行取中间索引时候,(i+j)/2. 一个是Integer.MAX_VALUE的一半,一个是MAX_VALUE就会超过正整数能表达的范围,就会得到一个负数。负数是补码的形式,符号位不变,数值为取反。所以会得到一个负数;java里面二进制数都是有符号的,最高位是符号位。
Q:为什么判断条件都写小于符号?
A:因为这里数组a是升序排列的,写成小于符号,相当于与数组排列的顺序是一致的。
二分查找的应用
重复元素
需求,如果存在重复元素,希望找到最左侧的第一个元素 这种形式称为LeftMost, 找最右侧的第一个元素,即为RightMost
首先,还是二分查找的解法,只不过在找到了的分支,追加向左区间继续找或向右区间继续找目标值的逻辑
/**
* 二分查找 - LeftMost
* 重复元素的数组中,查找最左侧的
*/
public static int binarySearchLeftMost(int[] a, int target) {
int i = 0, j = a.length - 1;
int candidate = -1; //候选
while (i <= j) {
int m = (i + j) >>> 1;
if (target < a[m]) {
j = m - 1;
} else if (a[m] < target) {
i = m + 1;
} else {
//只需要修改这里,找到目标需要存为候选,然后继续向左边找
candidate = m;
//继续向左边找,则需要设置右侧指针移至中间索引-1
j = m - 1;
}
}
return candidate;
}
/**
* 二分查找 - RightMost
* 重复元素的数组中,查找最右侧的
*/
public static int binarySearchRightMost(int[] a, int target) {
int i = 0, j = a.length - 1;
int candidate = -1; //候选
while (i <= j) {
int m = (i + j) >>> 1;
if (target < a[m]) {
j = m - 1;
} else if (a[m] < target) {
i = m + 1;
} else {
//只需要修改这里,找到目标需要存为候选,然后继续向右边找
candidate = m;
//继续向右边找,则需要设置左侧指针移至中间索引+1
i = m + 1;
}
}
return candidate;
}求排名
求排名,其实是LeftMost的应用,看一个图就了解了
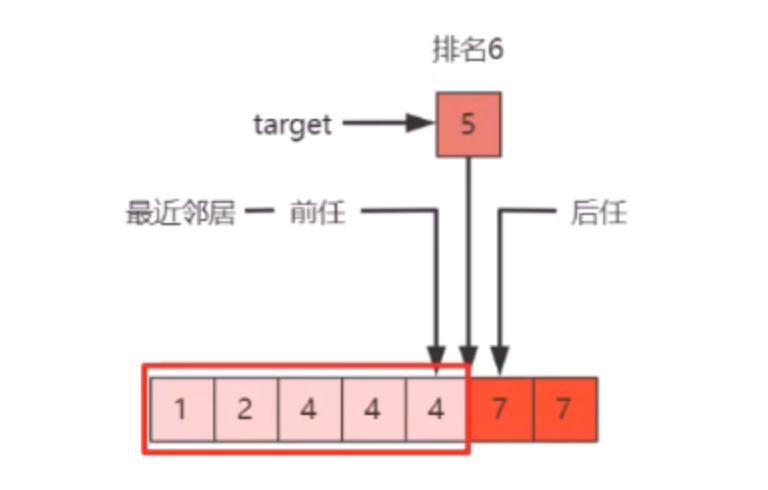
所以,求排名的解法就是:LeftMost+1。
求前任后任
还是这张图,也是最左和最右的应用。

分析可知, 求前任解法即:LeftMost-1 求后任解法即:RightMost+1
最近邻居
比如5的最近邻居是4,因为4和5差1,5和7差2, 就是找到前任和后任,然后比对,找到其中最小的。
范围查询
比如想找所有小于4的目标,0 .. LeftMost(4) - 1 比如找所有小于等于4的目标, 0 .. RightMost(4) 比如找所有大于4的目标, RightMost(4)+1 .. 无穷大 比如找所有大于等于4的目标,LeftMost(4) .. 无穷大 找 4 <= x <=7 ,LeftMost(4) .. RightMost(7) 找 4 < x <=7,RightMost(4)+1 .. LeftMost(7)-1
leetcode
抱一丝,仍然是leftMost和rightMost的应用,有了最左和最右就可以得到结果,
pubic int[] searchRange(int[] a, int target){
int left = leftMost(a, target);
if(left == -1){
return new int[]{-1, -1};
}else{
return new int[]{left, rightMost(a, traget)};
}
}