数据结构和算法之旅(五)- 栈
习惯来说,这一端称为栈顶,另一端不能操作数据的称为栈底,就如同生活中的一摞书籍。
定义
栈是一种线性数据结构,只能在其一端添加数据和移除数据。习惯来说,这一端称为栈顶,另一端不能操作数据的称为栈底,就如同生活中的一摞书籍。
还是老样子,看一下用不同方式实现栈。
/*先定义一个Stack接口*/
package org.example.datastructure;
public interface Stack<E> {
/**
* 向栈顶压入元素
* @param value 待压入元素
* @return 压入成功返回true,否则返回false
*/
boolean push(E value);
/**
* 从栈顶弹出元素
* @return 栈非空返回栈顶元素,否则返回null
*/
E pop();
/**
* 返回栈顶元素,但不弹出
* @return 栈非空返回栈顶元素,否则返回null
*/
E peek();
/**
* 判断栈是否为空
* @return 空返回true,否则返回false
*/
boolean isEmpty();
/**
* 判断栈是否已满
* @return 已满返回true,否则返回false
*/
boolean isFull();
}链表实现
package org.example.datastructure;
import java.util.Iterator;
/**
* 链表实现栈
* 含哨兵单向链表
*/
public class LinkedListStack<E> implements Stack<E>, Iterable<E> {
static class Node<E> {
E value;
Node<E> next;
public Node(E value, Node<E> next) {
this.value = value;
this.next = next;
}
}
private int capacity;
private int size;
/**
* 哨兵节点
*/
private Node<E> head = new Node<>(null, null);
public LinkedListStack(int capacity) {
this.capacity = capacity;
}
/**
* head -> 1 -> null
* head -> 2 -> 1 -> null
*/
@Override
public boolean push(E value) {
if (isFull()) return false;
// Node<E> added = new Node<>(value, head.next);
// head.next = added;
head.next = new Node<>(value, head.next);
size++;
return true;
}
@Override
public E pop() {
if (isEmpty()) return null;
Node<E> first = head.next;//找到第一个节点
head.next = first.next;//跳过(删除)第一个节点
size--;
return first.value;
}
@Override
public E peek() {
if (isEmpty()) return null;
Node<E> first = head.next;//找到第一个节点
return first.value;
}
@Override
public boolean isEmpty() {
// return head.next == null;
return size == 0;
}
@Override
public boolean isFull() {
return size == capacity;
}
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
Node<E> p = head.next;
@Override
public boolean hasNext() {
return p != null;
}
@Override
public E next() {
E value = p.value;
p = p.next;
return value;
}
};
}
}数组实现
package org.example.datastructure;
import java.util.Iterator;
public class ArrayStack<E> implements Stack<E>, Iterable<E> {
private final E[] array;
private int top;//栈顶指针
/**
* 底 顶
* 0 1 2 3 4
* 因为右边数组更好操作,与链表是反方向的
*/
@SuppressWarnings("all")
public ArrayStack(int capacity) {
this.array = (E[]) new Object[capacity];
}
@Override
public boolean push(E value) {
if (isFull()) return false;
array[top++] = value;
return true;
}
@Override
public E pop() {
if (isEmpty()) return null;
return array[--top];
}
@Override
public E peek() {
if (isEmpty()) return null;
return array[top - 1];
}
@Override
public boolean isEmpty() {
return top == 0;
}
@Override
public boolean isFull() {
return top == array.length;
}
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
int p = top;//指向栈顶,从右往左遍历
@Override
public boolean hasNext() {
return p > 0;
}
@Override
public E next() {
return array[--p];
}
};
}
}有效括号
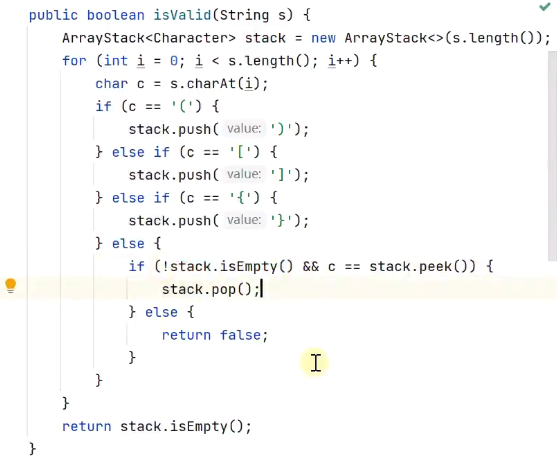
这个很简单:
遇到左括号,把要配对的右括号压入栈。
遇到右括号,把它与栈顶元素比对。
- 若相等,栈顶元素弹出,继续比对下一组。
- 若不等,无效括号直接返回false。
逆波兰表达式
1 + 2 ,这是中缀表达式。
1 2 +,这是后缀表达式。
后缀表达式交给计算机计算非常方便,因为从左向右计算,且不需要考虑优先级,优先级就是从左到右给定的顺序。

解题思路:
遇到数字就放入栈,如果遇到运算符就从栈中取出前俩个元素计算,计算结果再压入栈,栈中剩余的一个元素就是运算结果。
class Solution {
public int evalRPN(String[] tokens) {
LinkedList<Integer> stack = new LinkedList<>();
for (String t : tokens) {
switch (t) {
case "+" -> {
Integer b = stack.pop();
Integer a = stack.pop();
stack.push(a + b);
}
case "-" -> {
Integer b = stack.pop();
Integer a = stack.pop();
stack.push(a - b);
}
case "*" -> {
Integer b = stack.pop();
Integer a = stack.pop();
stack.push(a * b);
}
case "/" -> {
Integer b = stack.pop();
Integer a = stack.pop();
stack.push(a / b);
}
default -> {//数字
stack.push(Integer.parseInt(t));
}
}
}
return stack.pop();
}
}