数据结构和算法之旅(八)- 二叉搜索树
更高效的快速查找: 二叉搜索树
如果想实现快速查找,就得引入新的算法或者数据结构了。最早了解的二分查找算法查找效率不错,是logn的。但是排序也是成本比较高的,先排序再查找有些得不偿失。 那么有什么新的算法或数据结构呢,答案是有的,即二叉搜索树。
定义
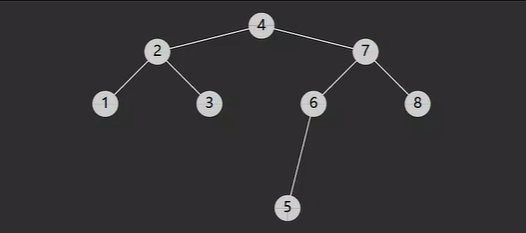
二叉搜索树有俩个特点:
1.树节点增加key属性,用来比较谁大谁小,key不可重复。
2.对于任意一个树节点,它的key比左子树的key都大,同时也比右子树的key都小。
性能
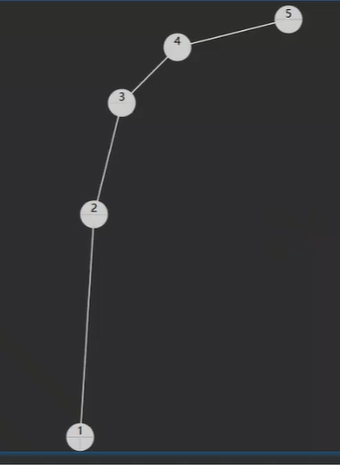
查找的性能是对数级别的,但是有些情况比如树不平衡的时候,时间复杂度又回到了O(n)。
code
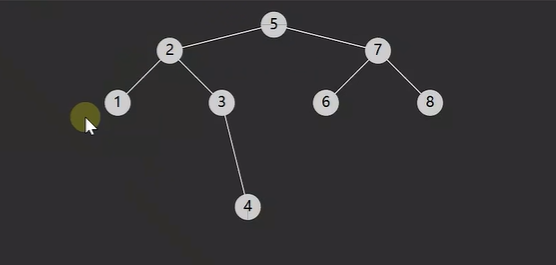
以下是几个提前准备的算法基础。
前任的算法

后任的算法(与前任相反) 
删除的算法(稍微复杂) 
package bst;
/**
* Binary Search Tree二叉搜索树
*/
public class BSTTree<K extends Comparable<K>, V> {
BSTNode<K, V> root;//根节点
static class BSTNode<K, V> {
K key;
V value;
BSTNode<K, V> left;
BSTNode<K, V> right;
public BSTNode(K key) {
this.key = key;
}
public BSTNode(K key, V value) {
this.key = key;
this.value = value;
}
public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
/**
* 查找关键字对应的值
*/
public V get(K key) {
//对外隐藏了BSTNode的参数,不用暴露给外界
return doGet(root, key);
}
/**
* 递归方式实现get
*/ private V doGet(BSTNode<K, V> p, K key) {
if (p == null) {
return null;//没有节点了,没找到,结束递归
}
int result = key.compareTo(p.key);
if (result < 0) {
return doGet(p.left, key);//如果待查找的key小于node,向左找
} else if (result > 0) {
return doGet(p.right, key);//向右找
} else {
return p.value;//找到了就返回value
}
}
/**
* 非递归实现get
* 尾递归的代码转换成非递归的实现非常简单,这样性能更好一些
* 比较java不支持尾递归自动优化,不妨都转换成循环的方式。
*/
public Object _get(K key) {
BSTNode<K, V> p = root;
while (p != null) {
int result = key.compareTo(p.key);
/*
compareTo -1 key < node.key 0 key == node.key 1 key > node.key */ if (result < 0) {
p = p.left;
} else if (result > 0) {
p = p.right;
} else {
return p.value;
}
}
return null;
}
/**
* 查找最小关键字的值
*/
public V min() {
return doMin(root);
}
/**
* 递归实现min
*/ public V doMin(BSTNode<K, V> node) {
if (node == null) return null;
if (node.left == null) {//最小节点
return node.value;
}
return doMin(node.left);
}
/**
* 非递归实现min
*/ public Object _doMin1(BSTNode node) {
if (node == null) return null;
while (node.left != null) {
node = node.left;
}
return node.value;
}
/**
* 查找最大关键字对应的值
* 最最小值类似,换找right即可,此处就省略了
*/
public V max() {
return _doMax(root);
}
/**
* 非递归实现max
*/ public V _doMax(BSTNode<K, V> node) {
if (node == null) return null;
while (node.right != null) {
node = node.right;
}
return node.value;
}
/**
* 存储关键字和对应值
* 先比较,再判断是更新还是新增
*/
public void put(K key, V value) {
//1.key存在,更新
//2.key不存在,新增
//get的实现拿过来
BSTNode<K, V> p = root;
BSTNode<K, V> parent = null;
while (p != null) {
parent = p;
int result = key.compareTo(p.key);
if (result < 0) {
p = p.left;
} else if (result > 0) {
p = p.right;
} else {
//找到了,更新
p.value = value;
return;
}
}
//没找到,新增
//父节点就是parent,因为if、else if变成null之后parent就是目标父节点
if (parent == null) {
root = new BSTNode<>(key, value);
}
int compareTo = key.compareTo(parent.key);
if (compareTo < 0) {
parent.left = new BSTNode<>(key, value);
} else if (compareTo > 0) {
parent.right = new BSTNode<>(key, value);
}
}
/**
* 查找关键字的前驱值(前任,比它小的里面最大的)
* 对二叉搜索树做一次中序遍历一下即可得到升序的结果,但这样不高效。
* <p>
* 而是要通过一下总结下来的规律得出的。
* 情况1:节点有左子树,此时前任就是左子树的最大值
* 情况2:节点没有左子树,若离它最近的、自左而来的祖先就是前任
*/
public V predecessor(K key) {
BSTNode<K, V> p = root;
BSTNode<K, V> fromLeft = null;
while (p != null) {
int result = key.compareTo(p.key);
if (result < 0) {
p = p.left;//向左走,祖先自右而来
} else if (result > 0) {
p = p.right;//向右走,祖先自左而来
fromLeft = p;
} else {
break;
}
}
//没找到节点
if (p == null) {
return null;
}
//情况1
if (p.left != null) {
return _doMax(p.left);//左子树最大值
}
//情况2
return fromLeft != null ? fromLeft.value : null;
}
/**
* 查找关键字的后驱值(后任,比它大的里面最小的)
*/
public V successor(K key) {
BSTNode<K, V> p = root;
BSTNode<K, V> fromRight = null;
while (p != null) {
int result = key.compareTo(p.key);
if (result < 0) {
p = p.left;//向左走,祖先自右而来
fromRight = p;
} else if (result > 0) {
p = p.right;//向右走,祖先自左而来
} else {
break;
}
}
//没找到节点
if (p == null) {
return null;
}
//情况1 节点有右子树,此时后任就是右子树的最小值
if (p.right != null) {
return doMin(p.right);//右子树最小值
}
//情况2 节点数没有右子树,若离它最近的、自右而来的祖先就是后任
return fromRight != null ? fromRight.value : null;
}
/**
* 根据关键字删除
* 核心概念:把被删除的节点的后继节点顶上去
*/
public V delete(K key) {
BSTNode<K, V> p = root;
BSTNode<K, V> parent = null;
while (p != null) {
int result = key.compareTo(p.key);
if (result < 0) {
parent = p;
p = p.left;//向左走,祖先自右而来
} else if (result > 0) {
parent = p;
p = p.right;//向右走,祖先自左而来
} else {
break;
}
}
if (p == null) return null;
//删除操作
if (p.left == null) {
//删除情况1(含情况3,走1,2都可以)
shift(parent, p, p.right);
} else if (p.right == null) {
//删除情况2
shift(parent, p, p.left);
} else {
//删除情况4
//4.1被删除节点找后继
BSTNode<K, V> s = p.right;
BSTNode<K, V> sPrent = p;//后继父亲
while (s.left != null) {
sPrent = s;
s = s.left;
}//s就是后继节点
//4.2删除节点与后继节点不相邻处理后继的后事
if (sPrent != p) {//不相邻
shift(sPrent, s, s.right);//不可能有左孩子
s.right = p.right;//顶上去的右
}
//4.3后继取代被删除节点
shift(parent, p, s);
s.left = p.left;//顶上去的左
}
return p.value;
}
/**
* 托孤方法 shift
* * @param parent 被删除节点的父节点
* @param deleted 被删除到节点
* @param child 被顶上去的节点
*/
private void shift(BSTNode<K, V> parent, BSTNode<K, V> deleted, BSTNode<K, V> child) {
if (parent == null) {
root = child;
} else if (deleted == parent.left) {
parent.left = child;
} else {
parent.right = child;
}
}
}