算法之旅2.0-图
如同交织万物的宏大网络,节点间由错综复杂的边线相连,描绘着无尽的关联与路径。它以这般灵活而强大的结构,揭示着信息间的复杂互动,是探索关系世界的导航图。
图(graph) 是一种非线性数据结构,由 顶点(vertex) 和 边(edge) 组成。我们可以将图 G 抽象地表示为一组顶点 V 和一组边 E 的集合。以下示例展示了一个包含 5 个顶点和 7 条边的图。

如果将顶点看作节点,将边看作连接各个节点的引用(指针),我们就可以将图看作一种从链表拓展而来的数据结构。如图所示, 相较于线性关系(链表)和分治关系(树),网络关系(图)的自由度更高 ,因而更为复杂。
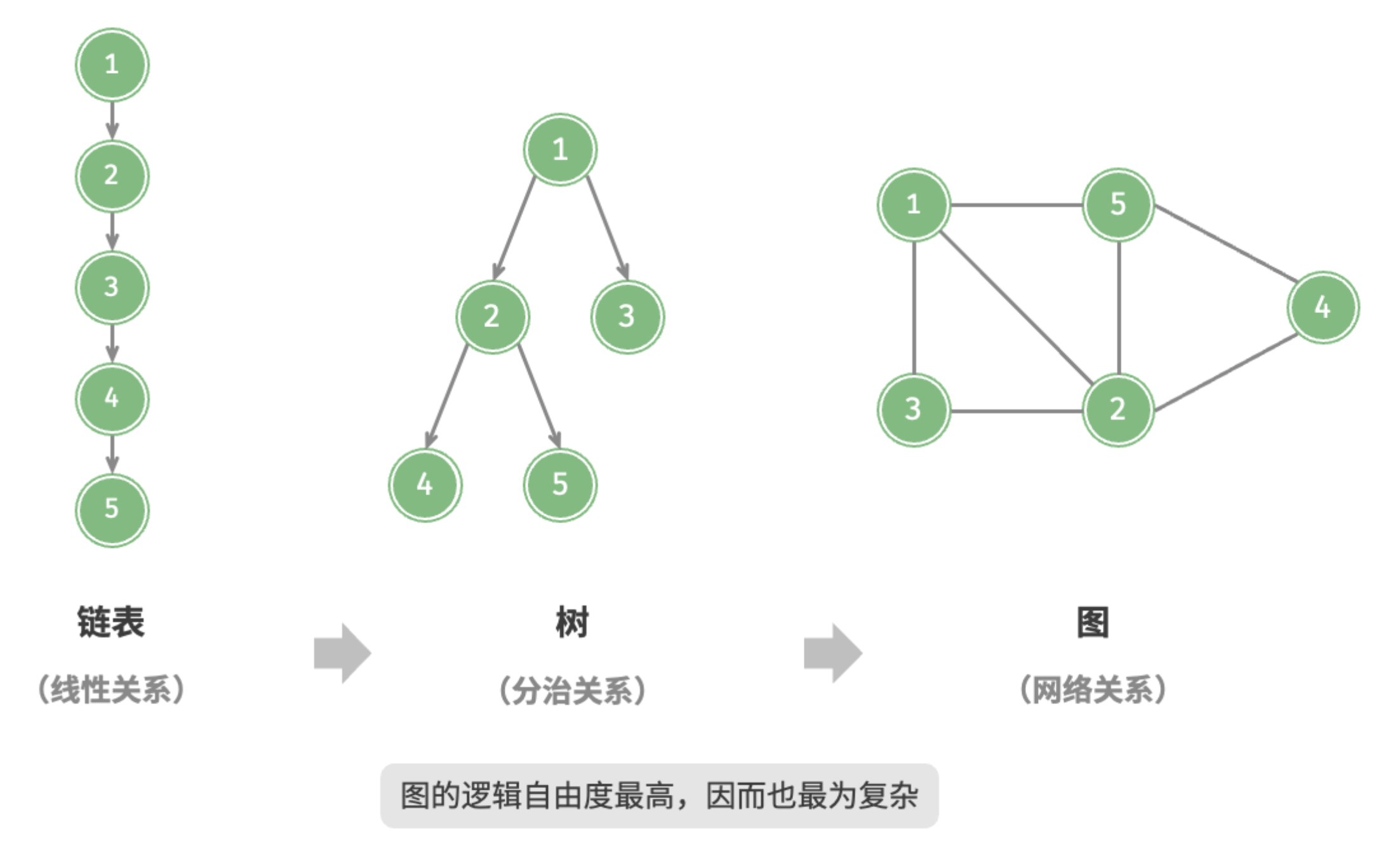
图的常见类型与术语
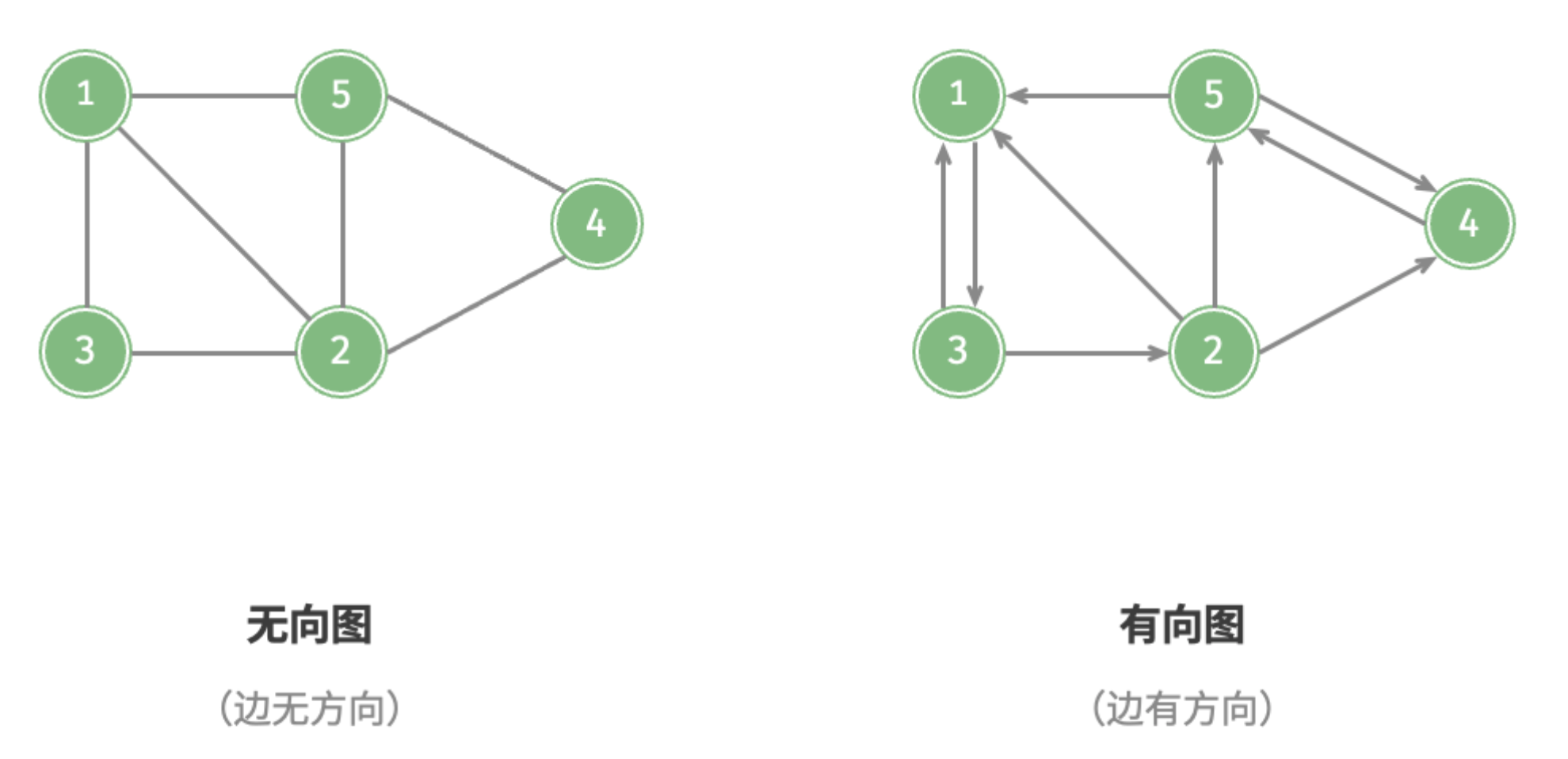
根据边是否具有方向,可分为 无向图(undirected graph) 和 有向图(directed graph) ,如图所示。
- 在无向图中,边表示两顶点之间的“双向”连接关系,例如微信或 QQ 中的“好友关系”。
- 在有向图中,边具有方向性,即 A→B 和 A←B 两个方向的边是相互独立的,例如微博或抖音上的“关注”与“被关注”关系。
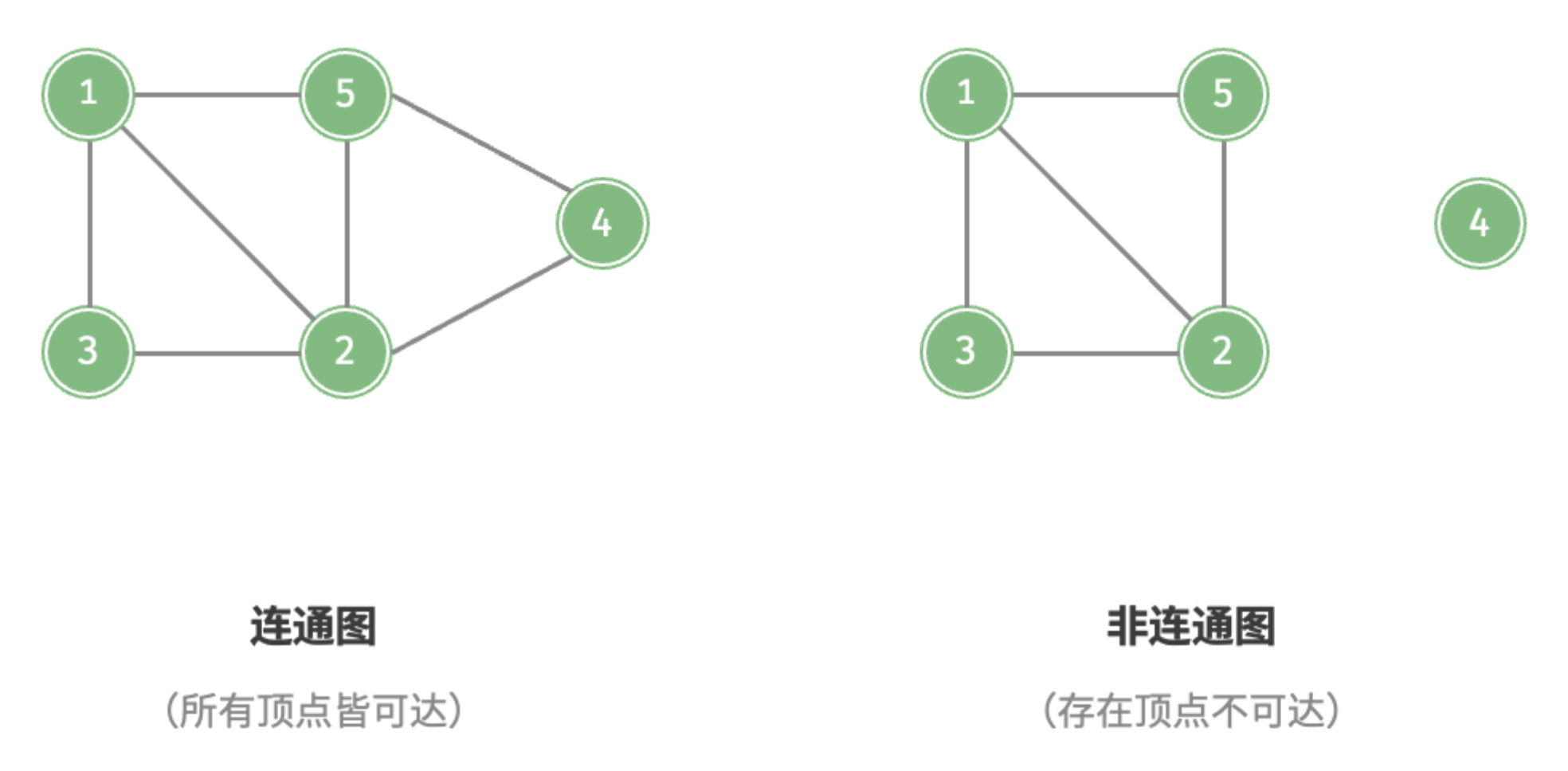
根据所有顶点是否连通,可分为 连通图(connected graph) 和 非连通图(disconnected graph) ,如图所示。
- 对于连通图,从某个顶点出发,可以到达其余任意顶点。
- 对于非连通图,从某个顶点出发,至少有一个顶点无法到达。
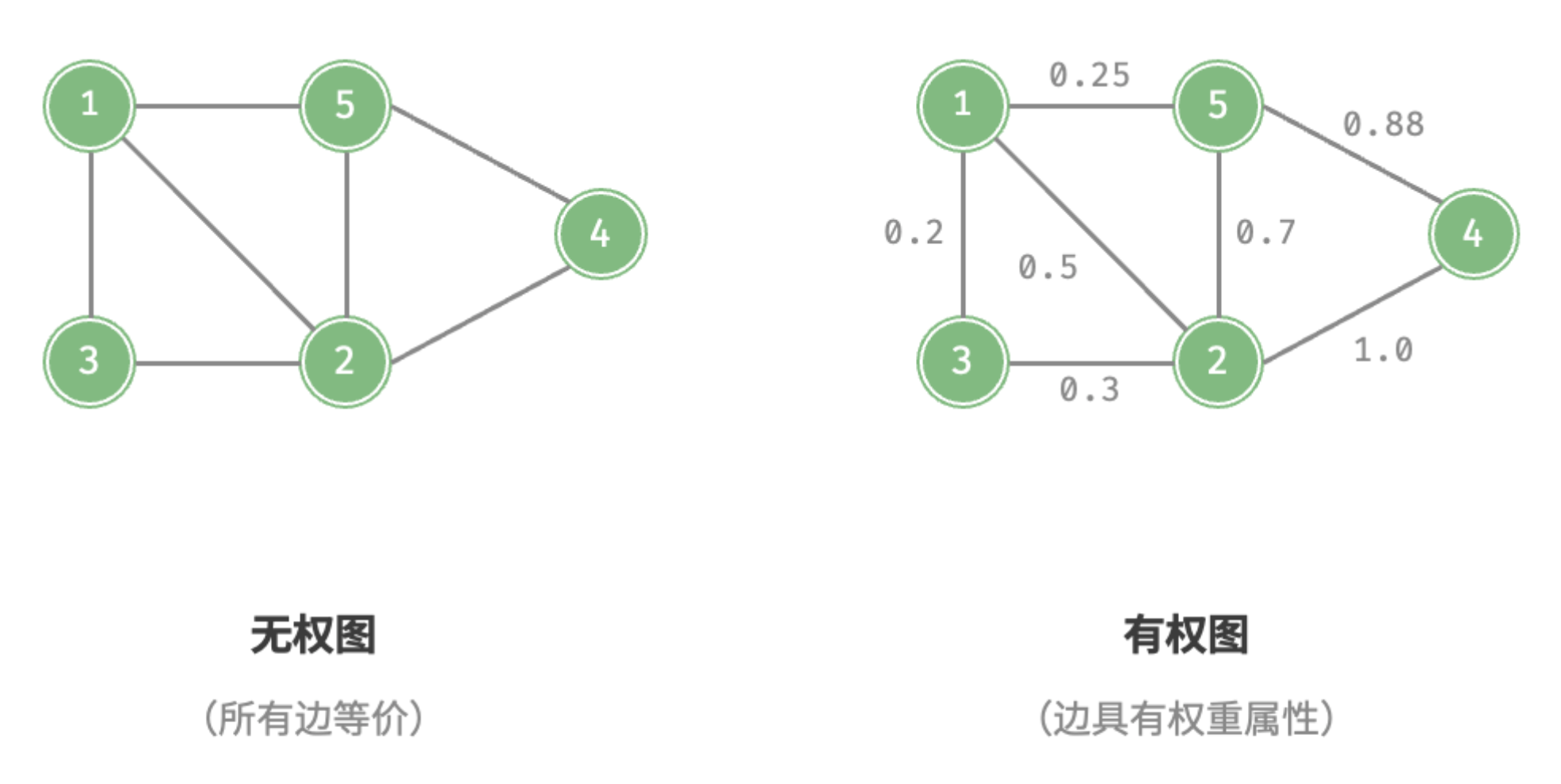
还可以为边添加“权重”变量,从而得到如图所示的 有权图(weighted graph) 。例如在《王者荣耀》等手游中,系统会根据共同游戏时间来计算玩家之间的“亲密度”,这种亲密度网络就可以用有权图来表示。
图数据结构包含以下常用术语。
- 邻接(adjacency) :当两顶点之间存在边相连时,称这两顶点“邻接”。在上图中,顶点 1 的邻接顶点为顶点 2、3、5。
- 路径(path) :从顶点 A 到顶点 B 经过的边构成的序列被称为从 A 到 B 的“路径”。在上图中,边序列 1-5-2-4 是顶点 1 到顶点 4 的一条路径。
- 度(degree) :一个顶点拥有的边数。对于有向图,入度(in-degree)表示有多少条边指向该顶点,出度(out-degree)表示有多少条边从该顶点指出。
图的表示
图的常用表示方式包括 “邻接矩阵” 和 “邻接表” 。以下使用无向图进行举例。
邻接矩阵
设图的顶点数量为 n ,邻接矩阵(adjacency matrix)使用一个 n∗n 大小的矩阵来表示图,每一行(列)代表一个顶点,矩阵元素代表边,用 1 或 0 表示两个顶点之间是否存在边。
如图所示,设邻接矩阵为 M、顶点列表为 V ,那么矩阵元素 M[i,j]=1 表示顶点 V[i] 到顶点 V[j] 之间存在边,反之 M[i,j]=0 表示两顶点之间无边。
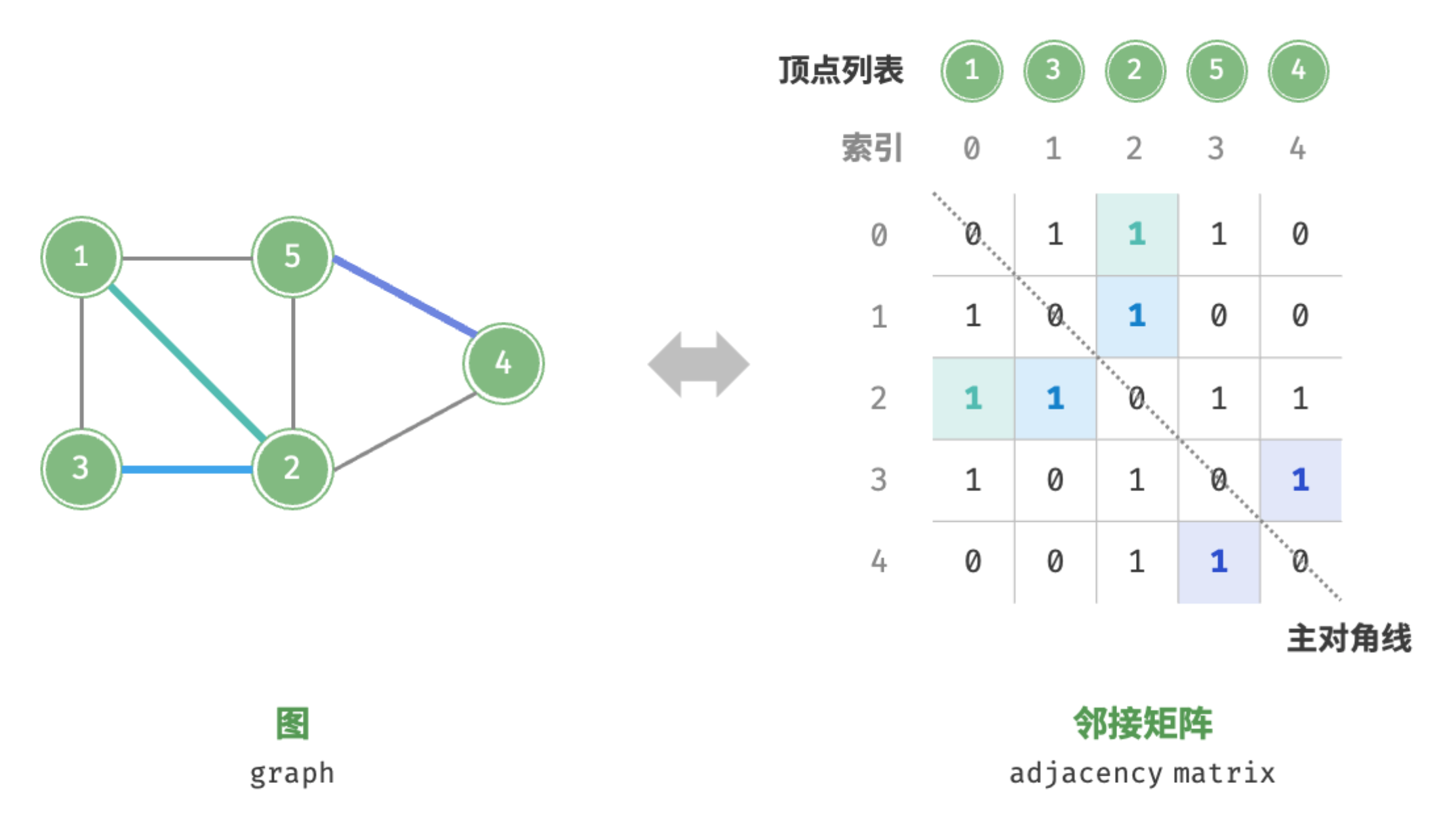
邻接矩阵具有以下特性。
- 在简单图中,顶点不能与自身相连,此时邻接矩阵主对角线元素没有意义。
- 对于无向图,两个方向的边等价,此时邻接矩阵关于主对角线对称。
- 将邻接矩阵的元素从 1 和 0 替换为权重,则可表示有权图。
使用邻接矩阵表示图时,我们可以直接访问矩阵元素以获取边,因此增删查改操作的效率很高,时间复杂度均为 O(1) 。然而,矩阵的空间复杂度为 O(n2) ,内存占用较多。
邻接表
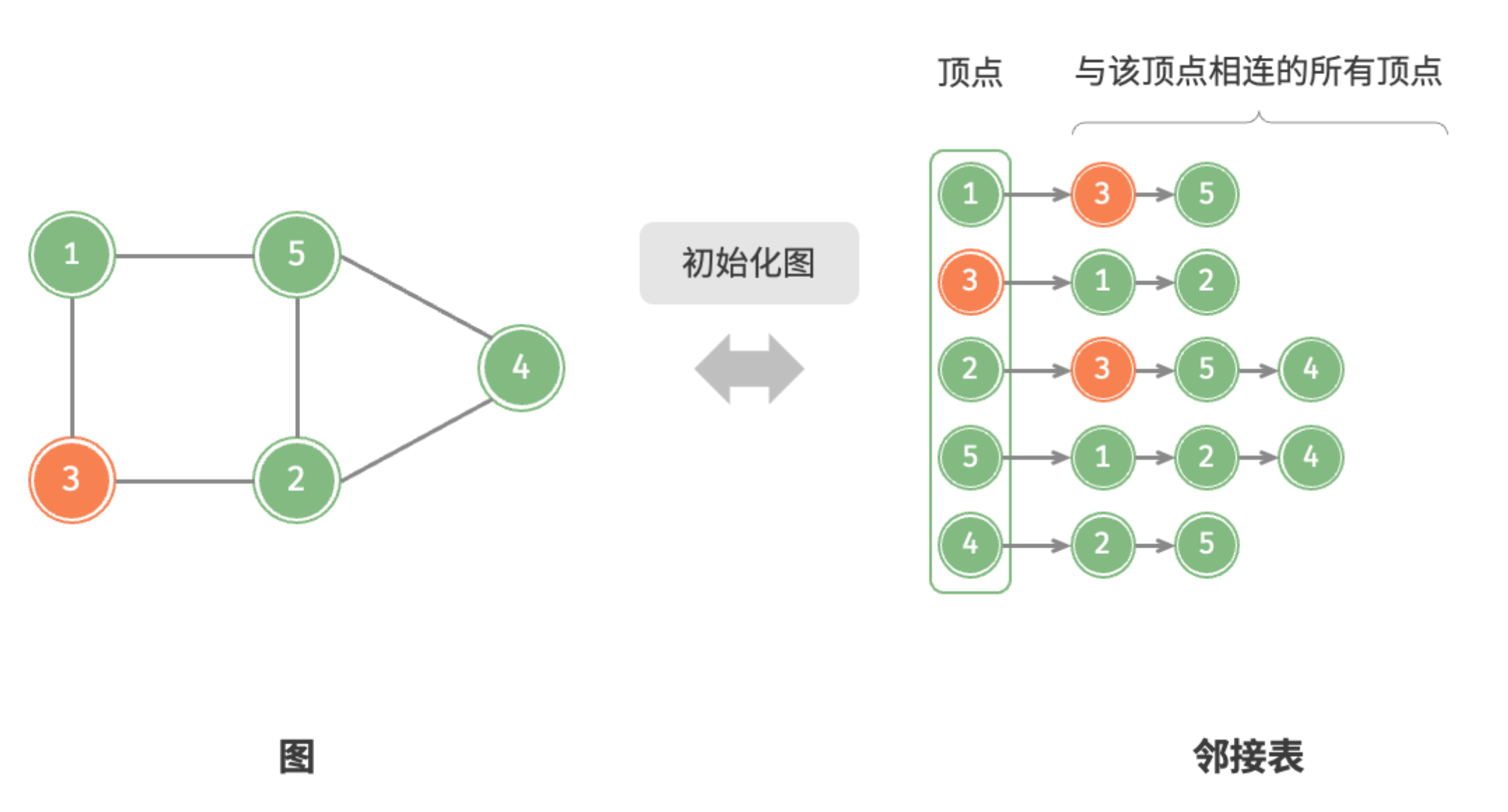
邻接表(adjacency list) 使用 n 个链表来表示图,链表节点表示顶点。第 i 个链表对应顶点 i ,其中存储了该顶点的所有邻接顶点(与该顶点相连的顶点)。下图展示了一个使用邻接表存储的图的示例。
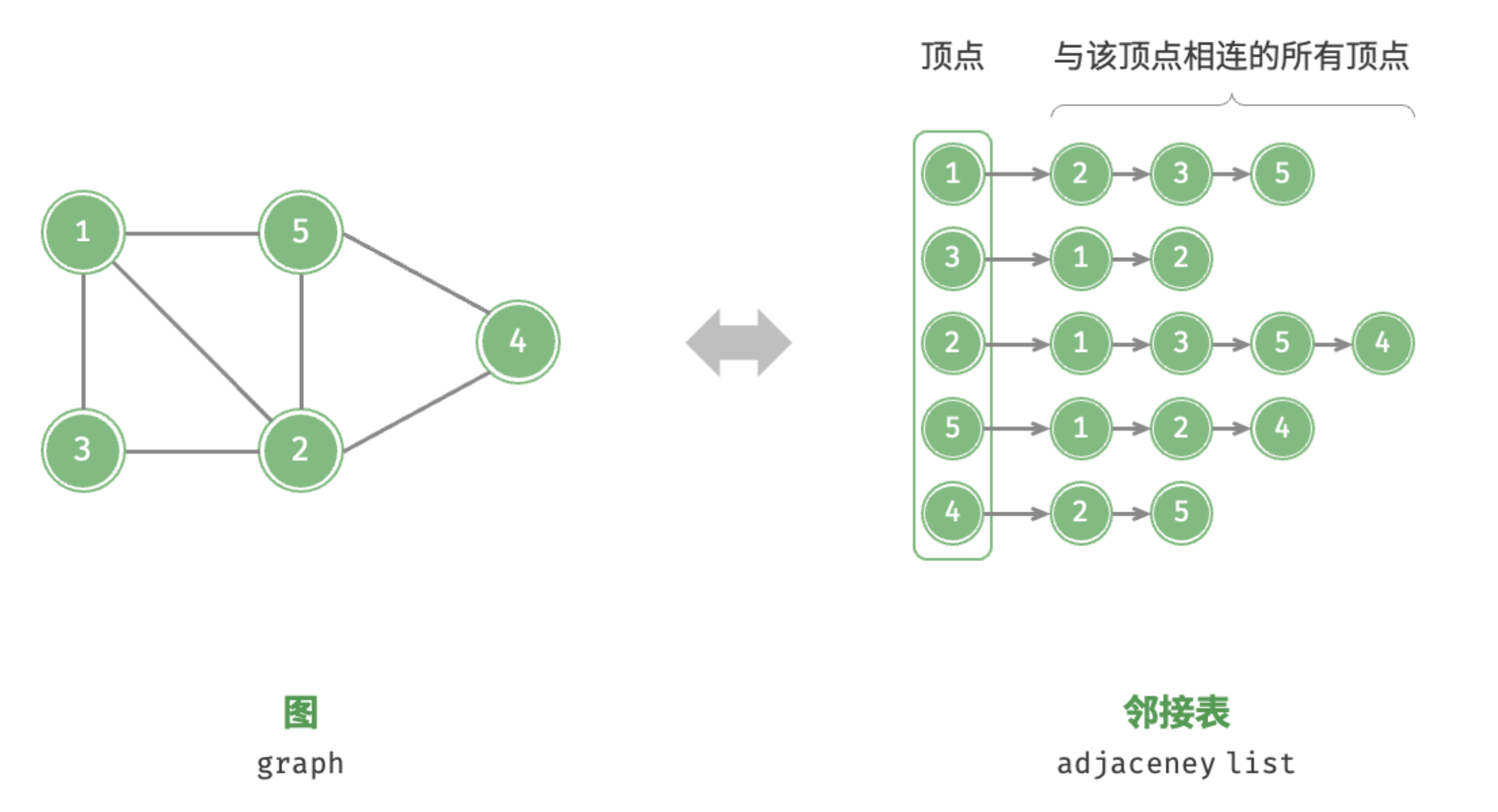
邻接表仅存储实际存在的边,而边的总数通常远小于 n2 ,因此它更加节省空间。然而,在邻接表中需要通过遍历链表来查找边,因此其时间效率不如邻接矩阵。
观察上图,邻接表结构与哈希表中的“链式地址”非常相似,因此我们也可以采用类似的方法来优化效率。 比如当链表较长时,可以将链表转化为 AVL 树或红黑树,从而将时间效率从 O(n) 优化至 O(logn) ;还可以把链表转换为哈希表,从而将时间复杂度降至 O(1) 。
图的常见应用
如表所示,许多现实系统可以用图来建模,相应的问题也可以约化为图计算问题。
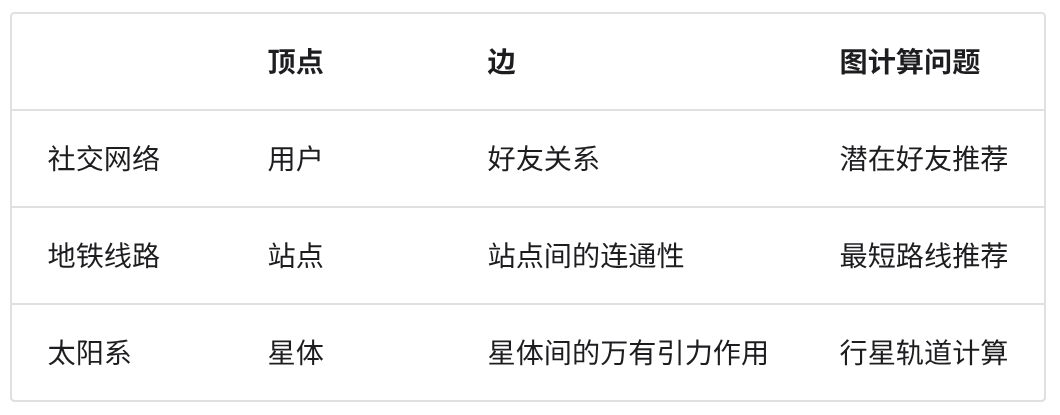
图的基础操作
图的基础操作可分为对“边”的操作和对“顶点”的操作。在“邻接矩阵”和“邻接表”两种表示方法下,实现方式有所不同。
基于邻接矩阵的实现
给定一个顶点数量为 n 的无向图,则各种操作的实现方式如图所示。
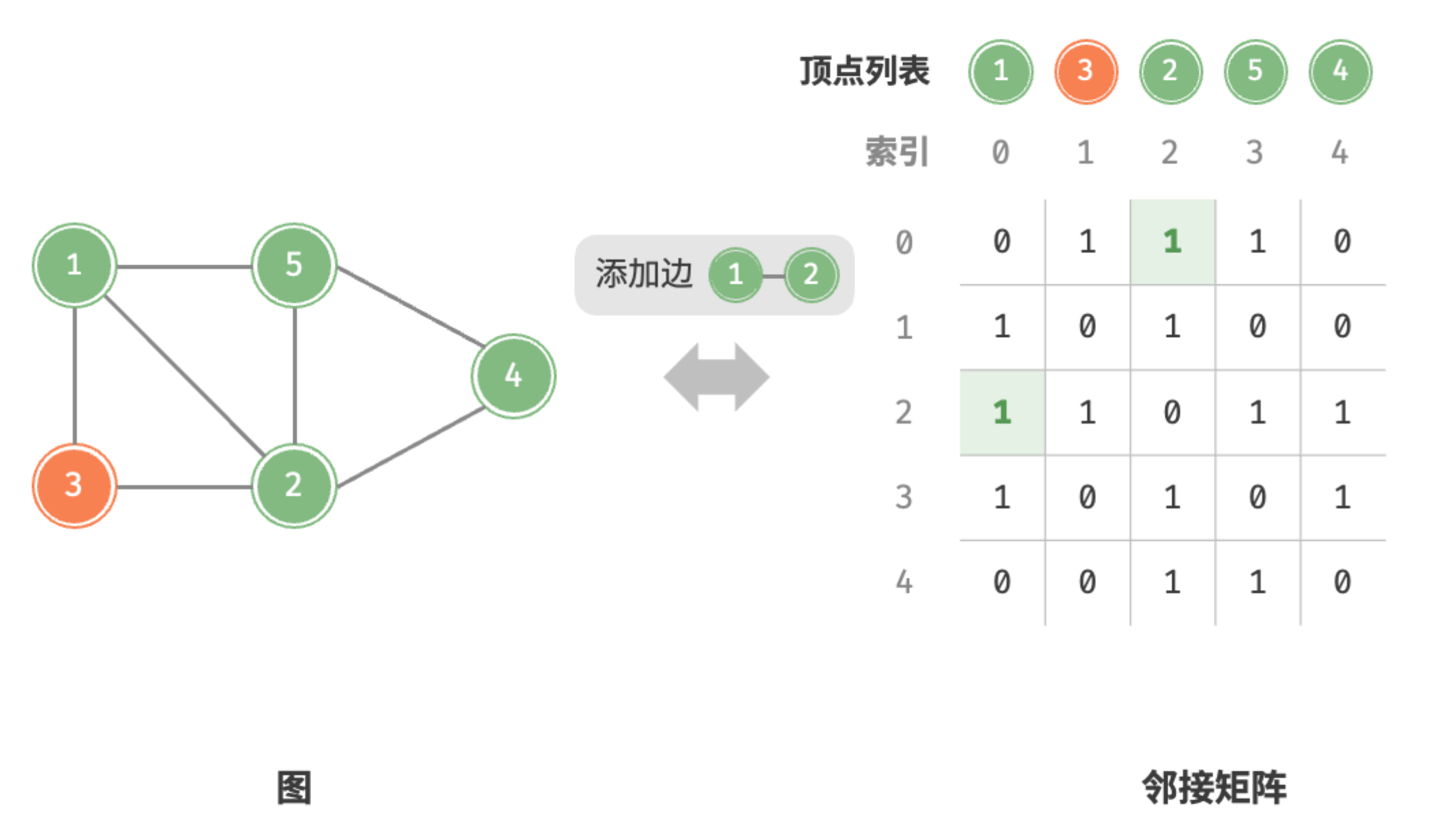
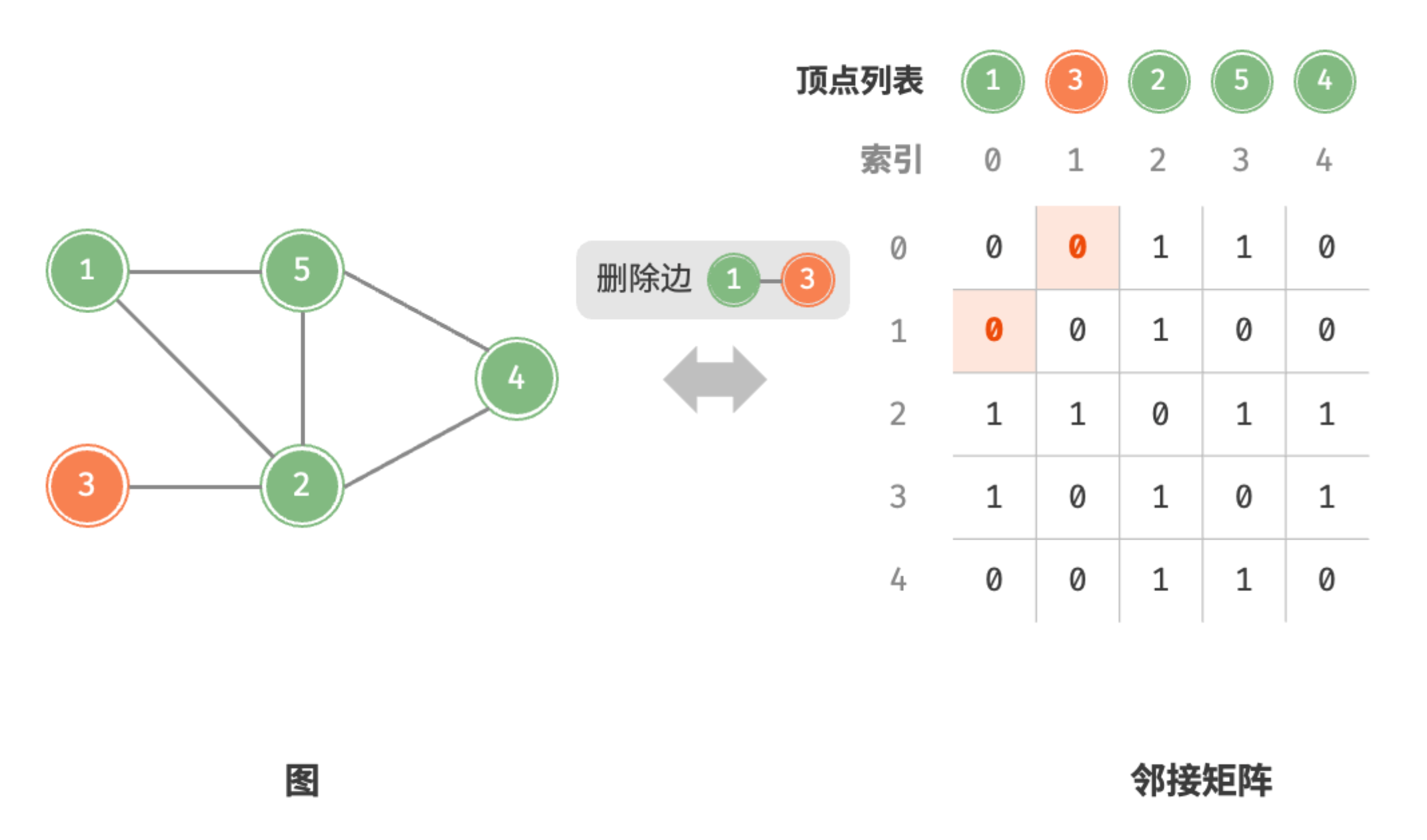
- 添加或删除边:直接在邻接矩阵中修改指定的边即可,使用 O(1) 时间。而由于是无向图,因此需要同时更新两个方向的边。
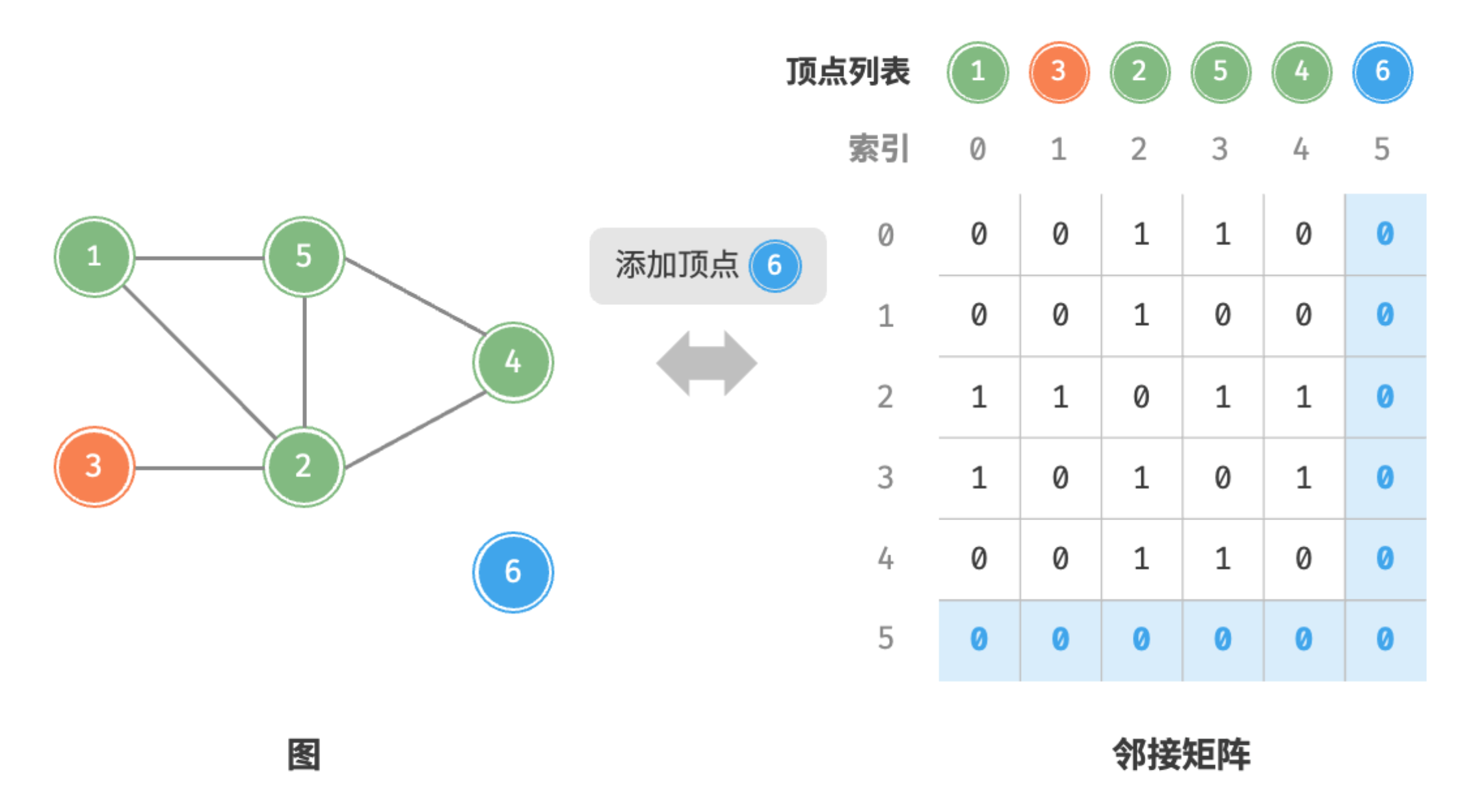
- 添加顶点:在邻接矩阵的尾部添加一行一列,并全部填 0 即可,使用 O(n) 时间。
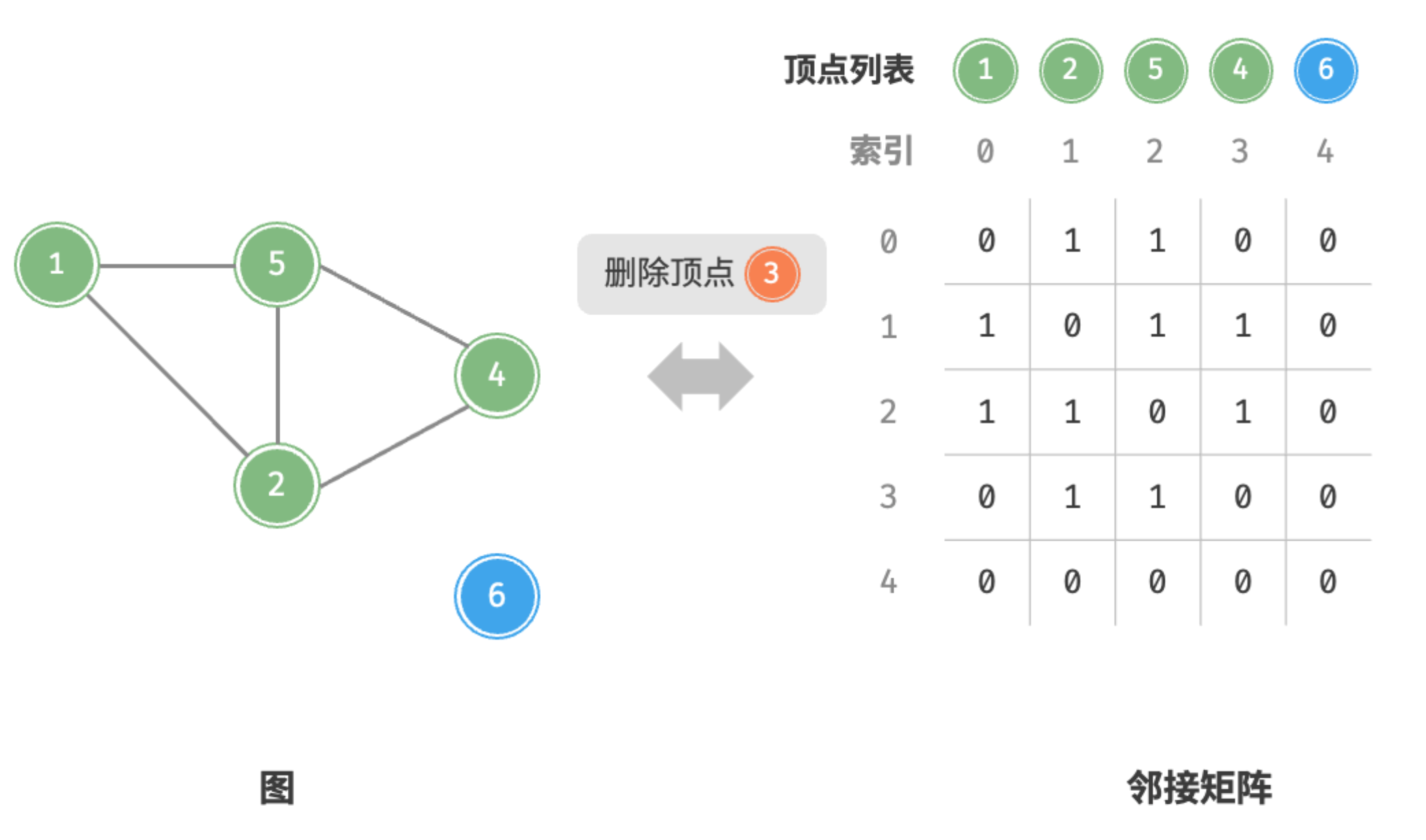
- 删除顶点:在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况,需要将 (n−1)2 个元素“向左上移动”,从而使用 O(n2) 时间。
- 初始化:传入 n 个顶点,初始化长度为 n 的顶点列表
vertices,使用 O(n) 时间;初始化 n∗n 大小的邻接矩阵adjMat,使用 O(n2) 时间。
初始化邻接矩阵
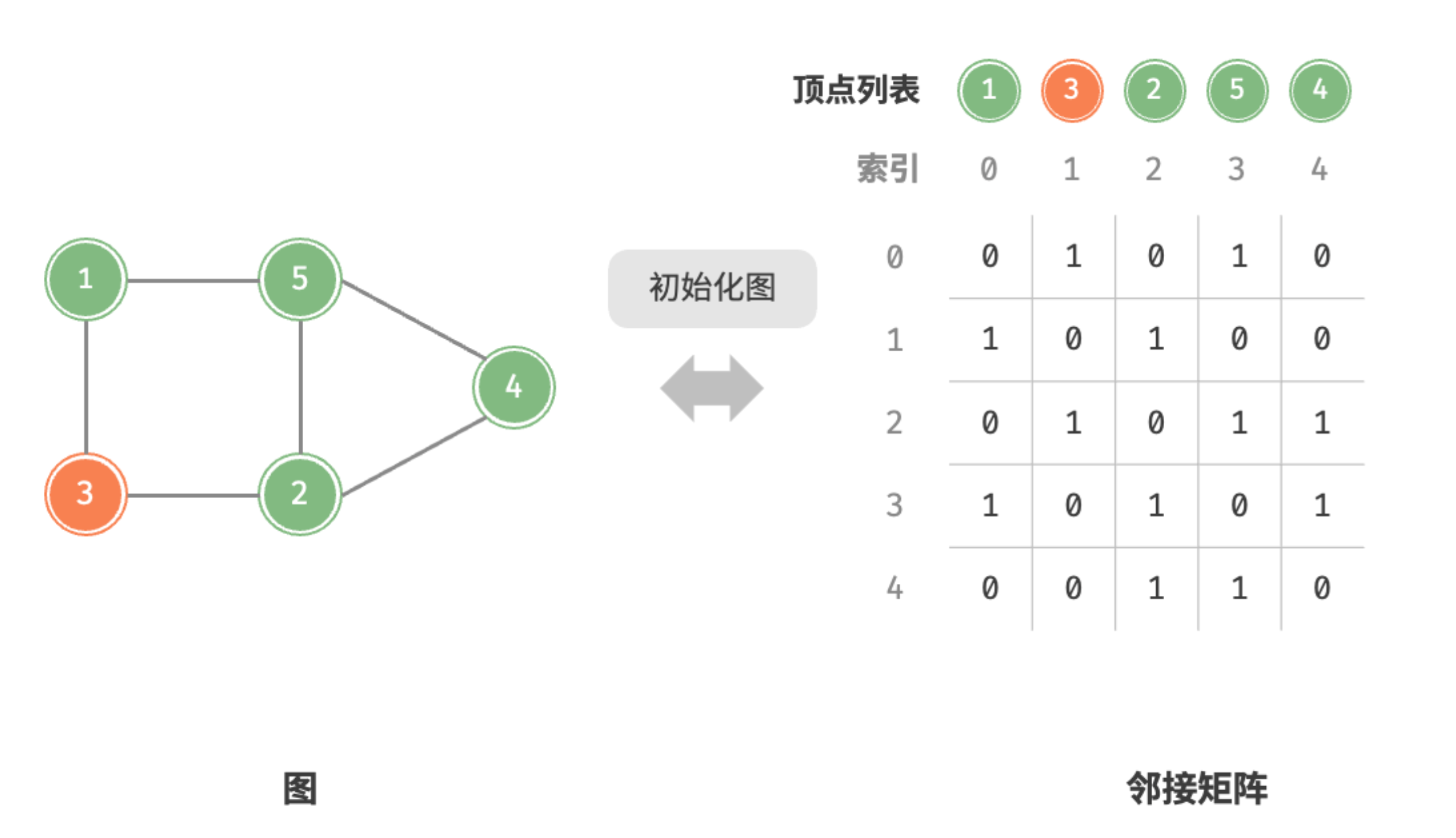
添加边
删除边
添加顶点
删除定点
结束
以下是基于邻接矩阵表示图的实现代码:
/* 基于邻接矩阵实现的无向图类 */
type graphAdjMat struct {
// 顶点列表,元素代表“顶点值”,索引代表“顶点索引”
vertices []int
// 邻接矩阵,行列索引对应“顶点索引”
adjMat [][]int
}
/* 构造函数 */
func newGraphAdjMat(vertices []int, edges [][]int) *graphAdjMat {
// 添加顶点
n := len(vertices)
adjMat := make([][]int, n)
for i := range adjMat {
adjMat[i] = make([]int, n)
}
// 初始化图
g := &graphAdjMat{
vertices: vertices,
adjMat: adjMat,
}
// 添加边
// 请注意,edges 元素代表顶点索引,即对应 vertices 元素索引
for i := range edges {
g.addEdge(edges[i][0], edges[i][1])
}
return g
}
/* 获取顶点数量 */
func (g *graphAdjMat) size() int {
return len(g.vertices)
}
/* 添加顶点 */
func (g *graphAdjMat) addVertex(val int) {
n := g.size()
// 向顶点列表中添加新顶点的值
g.vertices = append(g.vertices, val)
// 在邻接矩阵中添加一行
newRow := make([]int, n)
g.adjMat = append(g.adjMat, newRow)
// 在邻接矩阵中添加一列
for i := range g.adjMat {
g.adjMat[i] = append(g.adjMat[i], 0)
}
}
/* 删除顶点 */
func (g *graphAdjMat) removeVertex(index int) {
if index >= g.size() {
return
}
// 在顶点列表中移除索引 index 的顶点
g.vertices = append(g.vertices[:index], g.vertices[index+1:]...)
// 在邻接矩阵中删除索引 index 的行
g.adjMat = append(g.adjMat[:index], g.adjMat[index+1:]...)
// 在邻接矩阵中删除索引 index 的列
for i := range g.adjMat {
g.adjMat[i] = append(g.adjMat[i][:index], g.adjMat[i][index+1:]...)
}
}
/* 添加边 */
// 参数 i, j 对应 vertices 元素索引
func (g *graphAdjMat) addEdge(i, j int) {
// 索引越界与相等处理
if i < 0 || j < 0 || i >= g.size() || j >= g.size() || i == j {
fmt.Errorf("%s", "Index Out Of Bounds Exception")
}
// 在无向图中,邻接矩阵关于主对角线对称,即满足 (i, j) == (j, i)
g.adjMat[i][j] = 1
g.adjMat[j][i] = 1
}
/* 删除边 */
// 参数 i, j 对应 vertices 元素索引
func (g *graphAdjMat) removeEdge(i, j int) {
// 索引越界与相等处理
if i < 0 || j < 0 || i >= g.size() || j >= g.size() || i == j {
fmt.Errorf("%s", "Index Out Of Bounds Exception")
}
g.adjMat[i][j] = 0
g.adjMat[j][i] = 0
}
/* 打印邻接矩阵 */
func (g *graphAdjMat) print() {
fmt.Printf("\t顶点列表 = %v\n", g.vertices)
fmt.Printf("\t邻接矩阵 = \n")
for i := range g.adjMat {
fmt.Printf("\t\t\t%v\n", g.adjMat[i])
}
}基于邻接表的实现
设无向图的顶点总数为 n、边总数为 m ,则可根据图中所示的方法实现各种操作。
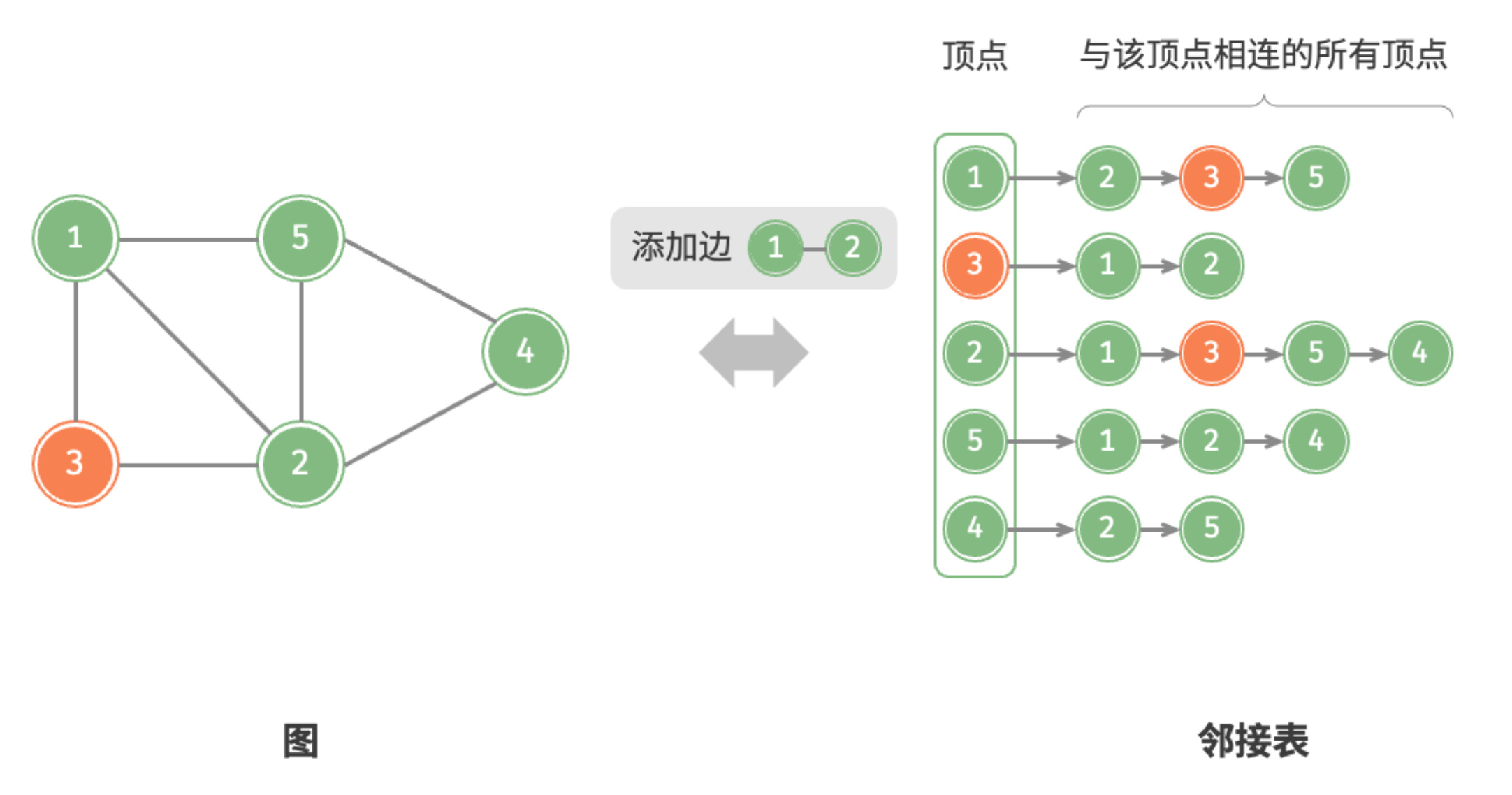
- 添加边:在顶点对应链表的末尾添加边即可,使用 O(1) 时间。因为是无向图,所以需要同时添加两个方向的边。
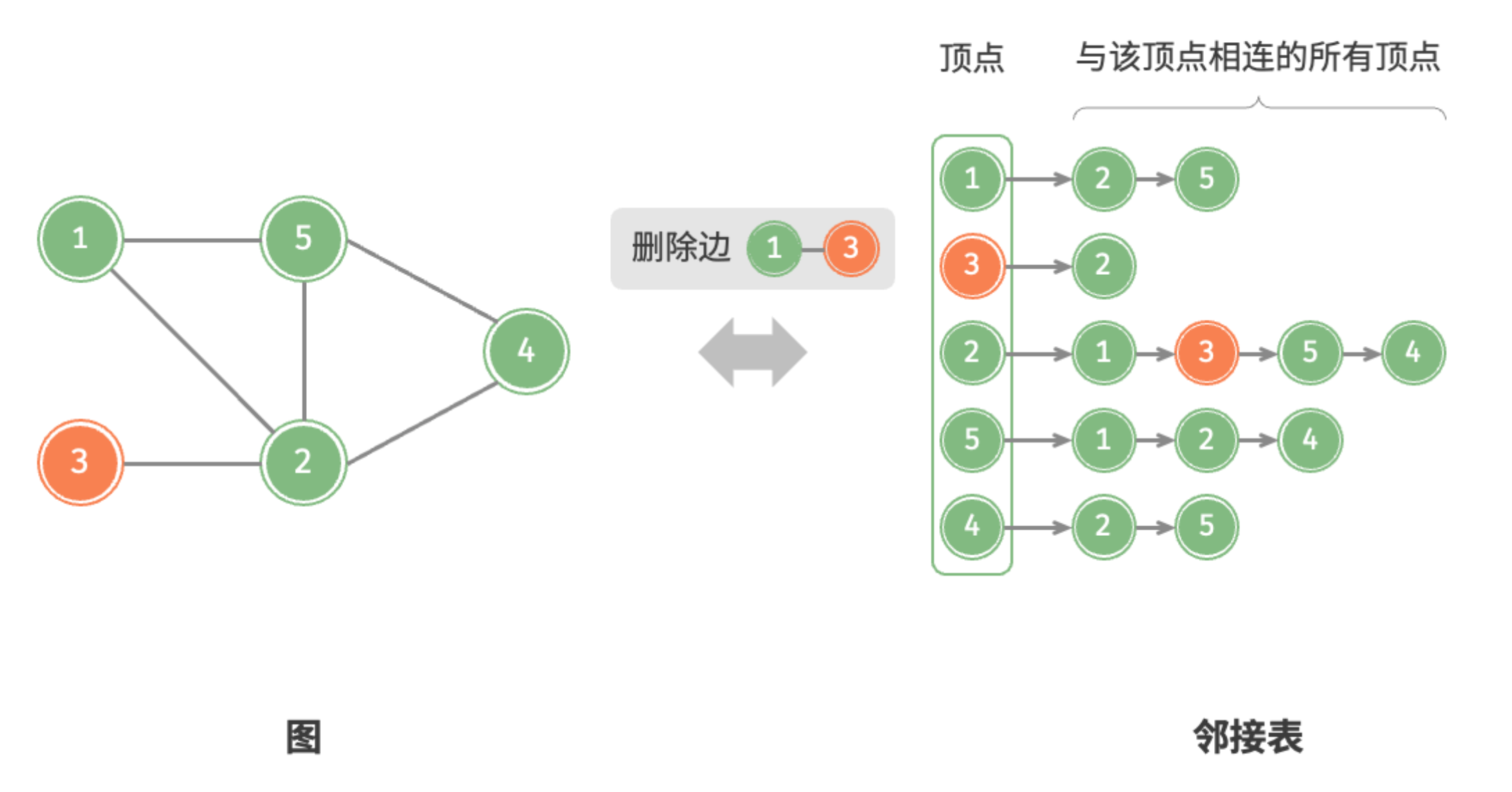
- 删除边:在顶点对应链表中查找并删除指定边,使用 O(m) 时间。在无向图中,需要同时删除两个方向的边。
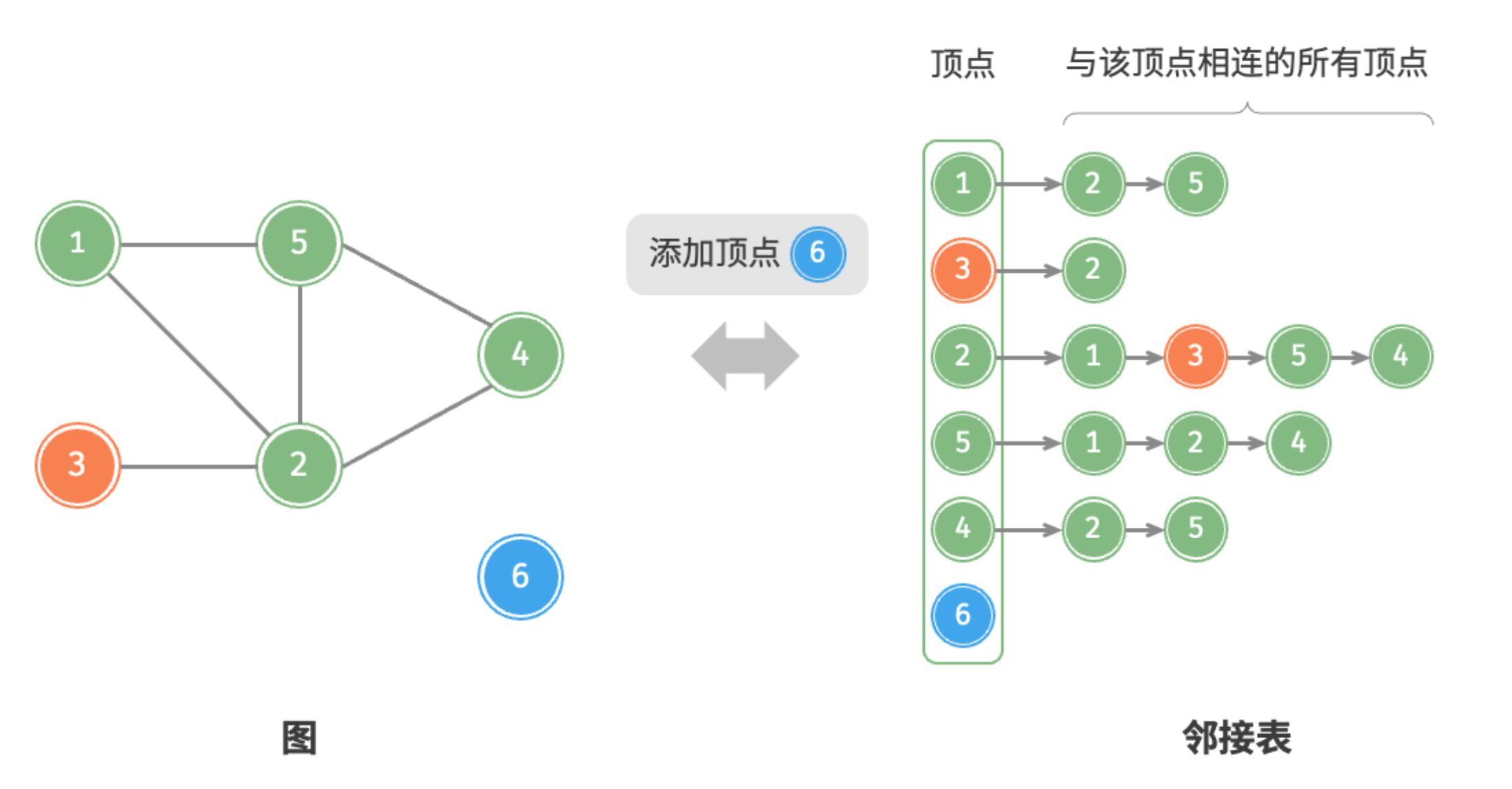
- 添加顶点:在邻接表中添加一个链表,并将新增顶点作为链表头节点,使用 O(1) 时间。
- 删除顶点:需遍历整个邻接表,删除包含指定顶点的所有边,使用 O(n+m) 时间。
- 初始化:在邻接表中创建 n 个顶点和 2m 条边,使用 O(n+m) 时间。
初始化邻接表
添加边
删除边
添加顶点
结束
以下是邻接表的代码实现。对比上图,实际代码有以下不同。
- 为了方便添加与删除顶点,以及简化代码,我们使用列表(动态数组)来代替链表。
- 使用哈希表来存储邻接表,
key为顶点实例,value为该顶点的邻接顶点列表(链表)。
另外,我们在邻接表中使用 Vertex 类来表示顶点,这样做的原因是:如果与邻接矩阵一样,用列表索引来区分不同顶点,那么假设要删除索引为 i 的顶点,则需遍历整个邻接表,将所有大于 i 的索引全部减 1 ,效率很低。而如果每个顶点都是唯一的 Vertex 实例,删除某一顶点之后就无须改动其他顶点了。
/* 基于邻接表实现的无向图类 */
type graphAdjList struct {
// 邻接表,key:顶点,value:该顶点的所有邻接顶点
adjList map[Vertex][]Vertex
}
/* 构造函数 */
func newGraphAdjList(edges [][]Vertex) *graphAdjList {
g := &graphAdjList{
adjList: make(map[Vertex][]Vertex),
}
// 添加所有顶点和边
for _, edge := range edges {
g.addVertex(edge[0])
g.addVertex(edge[1])
g.addEdge(edge[0], edge[1])
}
return g
}
/* 获取顶点数量 */
func (g *graphAdjList) size() int {
return len(g.adjList)
}
/* 添加边 */
func (g *graphAdjList) addEdge(vet1 Vertex, vet2 Vertex) {
_, ok1 := g.adjList[vet1]
_, ok2 := g.adjList[vet2]
if !ok1 || !ok2 || vet1 == vet2 {
panic("error")
}
// 添加边 vet1 - vet2, 添加匿名 struct{},
g.adjList[vet1] = append(g.adjList[vet1], vet2)
g.adjList[vet2] = append(g.adjList[vet2], vet1)
}
/* 删除边 */
func (g *graphAdjList) removeEdge(vet1 Vertex, vet2 Vertex) {
_, ok1 := g.adjList[vet1]
_, ok2 := g.adjList[vet2]
if !ok1 || !ok2 || vet1 == vet2 {
panic("error")
}
// 删除边 vet1 - vet2
g.adjList[vet1] = DeleteSliceElms(g.adjList[vet1], vet2)
g.adjList[vet2] = DeleteSliceElms(g.adjList[vet2], vet1)
}
/* 添加顶点 */
func (g *graphAdjList) addVertex(vet Vertex) {
_, ok := g.adjList[vet]
if ok {
return
}
// 在邻接表中添加一个新链表
g.adjList[vet] = make([]Vertex, 0)
}
/* 删除顶点 */
func (g *graphAdjList) removeVertex(vet Vertex) {
_, ok := g.adjList[vet]
if !ok {
panic("error")
}
// 在邻接表中删除顶点 vet 对应的链表
delete(g.adjList, vet)
// 遍历其他顶点的链表,删除所有包含 vet 的边
for v, list := range g.adjList {
g.adjList[v] = DeleteSliceElms(list, vet)
}
}
/* 打印邻接表 */
func (g *graphAdjList) print() {
var builder strings.Builder
fmt.Printf("邻接表 = \n")
for k, v := range g.adjList {
builder.WriteString("\t\t" + strconv.Itoa(k.Val) + ": ")
for _, vet := range v {
builder.WriteString(strconv.Itoa(vet.Val) + " ")
}
fmt.Println(builder.String())
builder.Reset()
}
}效率对比
设图中共有 n 个顶点和 m 条边,下表对比了邻接矩阵和邻接表的时间效率和空间效率。请注意,邻接表(链表)对应本文实现,而邻接表(哈希表)专指将所有链表替换为哈希表后的实现。
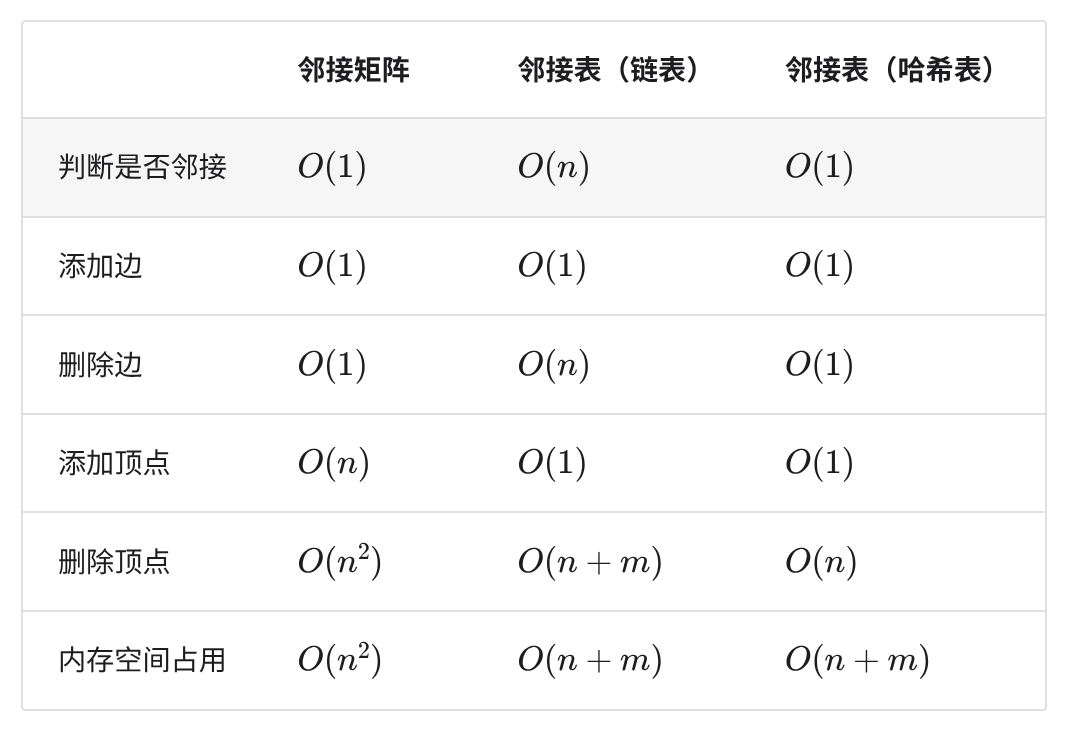
观察表,似乎邻接表(哈希表)的时间效率与空间效率最优。但实际上,在邻接矩阵中操作边的效率更高,只需一次数组访问或赋值操作即可。综合来看,邻接矩阵体现了“以空间换时间”的原则,而邻接表体现了“以时间换空间”的原则。
图的遍历
树代表的是“一对多”的关系,而图则具有更高的自由度,可以表示任意的“多对多”关系。因此,我们可以把树看作图的一种特例。显然,树的遍历操作也是图的遍历操作的一种特例。
图和树都需要应用搜索算法来实现遍历操作。图的遍历方式也可分为两种:广度优先遍历和深度优先遍历。
广度优先遍历
广度优先遍历是一种由近及远的遍历方式,从某个节点出发,始终优先访问距离最近的顶点,并一层层向外扩张。 如图所示,从左上角顶点出发,首先遍历该顶点的所有邻接顶点,然后遍历下一个顶点的所有邻接顶点,以此类推,直至所有顶点访问完毕。
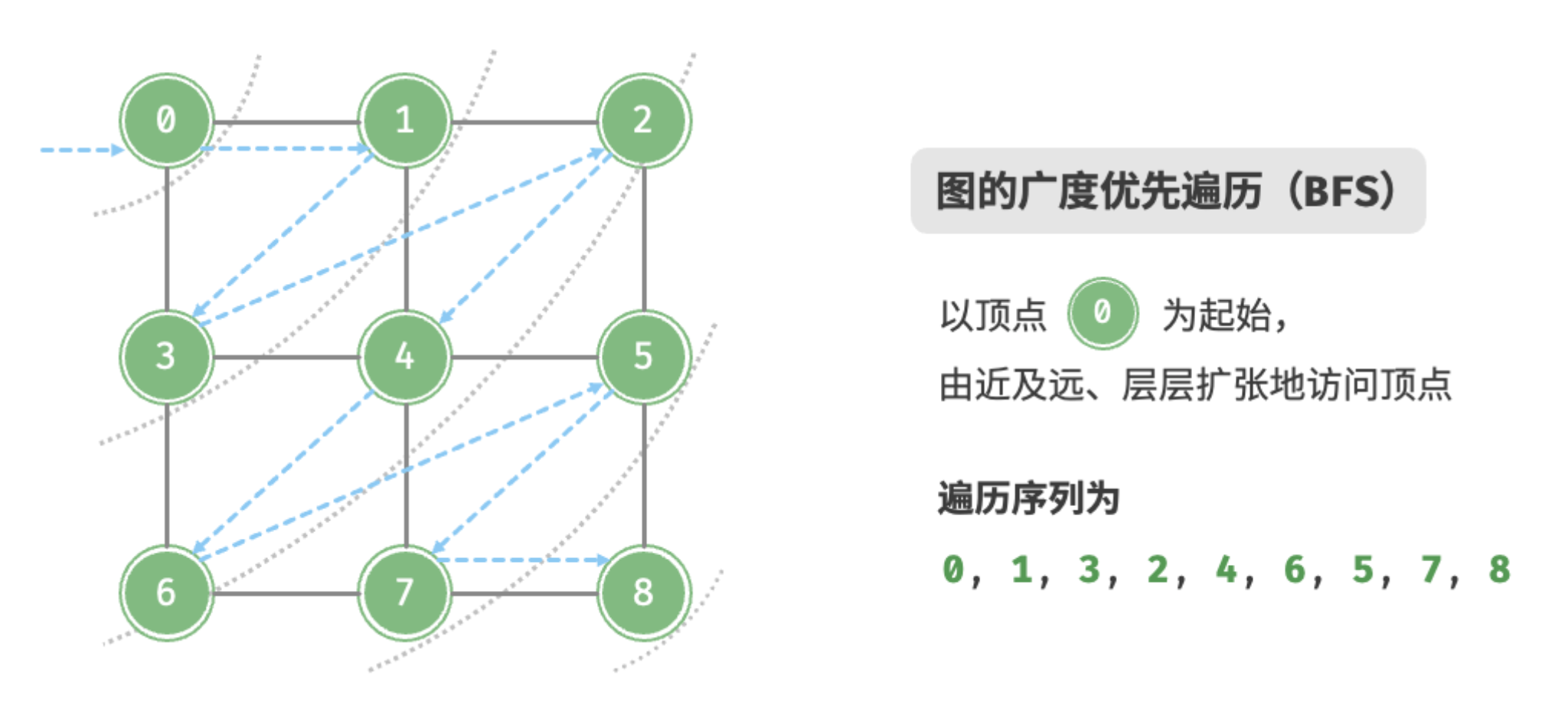
算法实现
BFS 通常借助队列来实现,代码如下所示。队列具有“先入先出”的性质,这与 BFS 的“由近及远”的思想异曲同工。
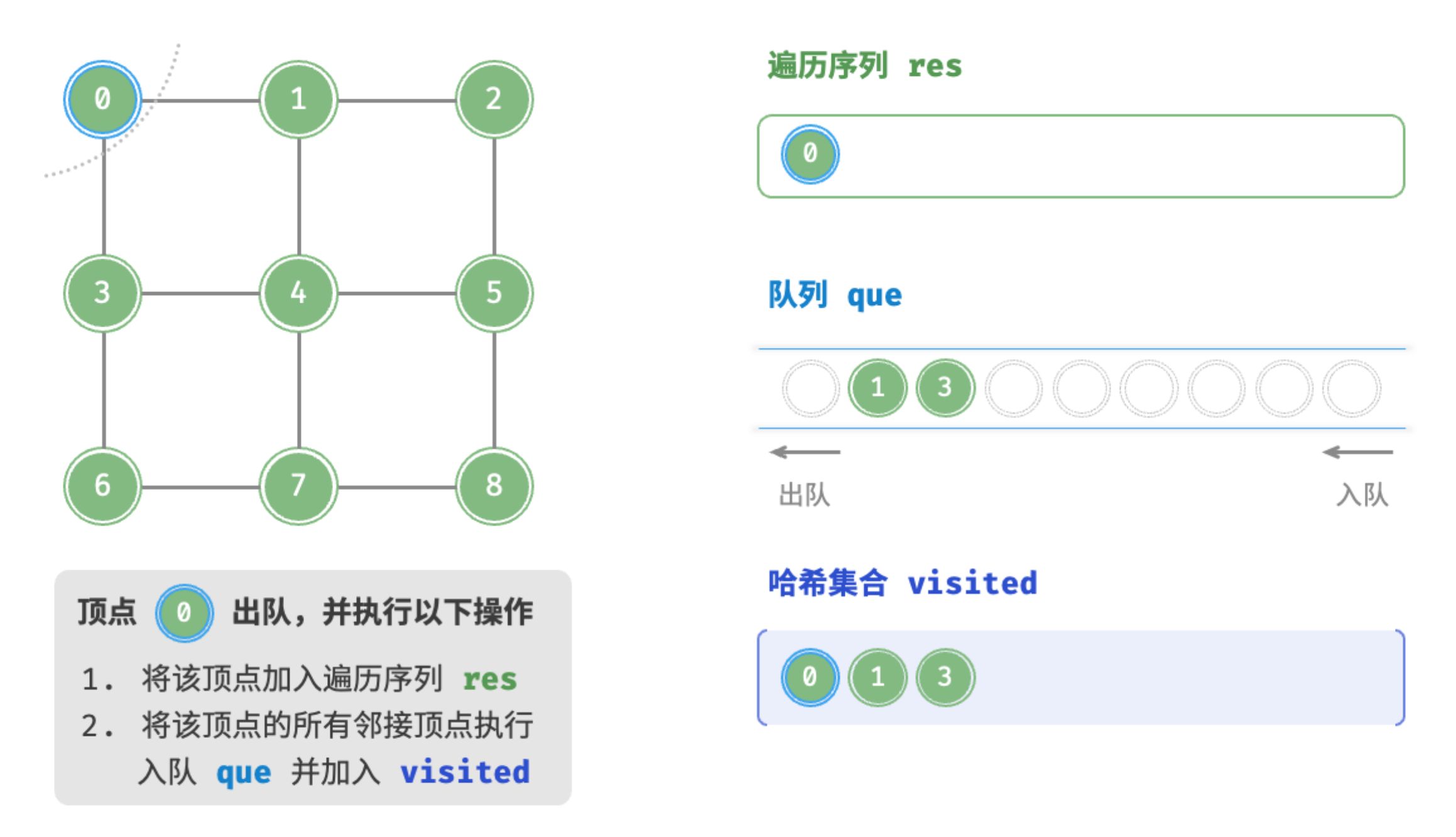
- 将遍历起始顶点
startVet加入队列,并开启循环。 - 在循环的每轮迭代中,弹出队首顶点并记录访问,然后将该顶点的所有邻接顶点加入到队列尾部。
- 循环步骤
2.,直到所有顶点被访问完毕后结束。
为了防止重复遍历顶点,我们需要借助一个哈希集合 visited 来记录哪些节点已被访问。
提示
哈希集合可以看作一个只存储 key 而不存储 value 的哈希表,它可以在 O(1) 时间复杂度下进行 key 的增删查改操作。根据 key 的唯一性,哈希集合通常用于数据去重等场景。
/* 广度优先遍历 */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
func graphBFS(g *graphAdjList, startVet Vertex) []Vertex {
// 顶点遍历序列
res := make([]Vertex, 0)
// 哈希集合,用于记录已被访问过的顶点
visited := make(map[Vertex]struct{})
visited[startVet] = struct{}{}
// 队列用于实现 BFS, 使用切片模拟队列
queue := make([]Vertex, 0)
queue = append(queue, startVet)
// 以顶点 vet 为起点,循环直至访问完所有顶点
for len(queue) > 0 {
// 队首顶点出队
vet := queue[0]
queue = queue[1:]
// 记录访问顶点
res = append(res, vet)
// 遍历该顶点的所有邻接顶点
for _, adjVet := range g.adjList[vet] {
_, isExist := visited[adjVet]
// 只入队未访问的顶点
if !isExist {
queue = append(queue, adjVet)
visited[adjVet] = struct{}{}
}
}
}
// 返回顶点遍历序列
return res
}代码相对抽象,建议对照图来加深理解。
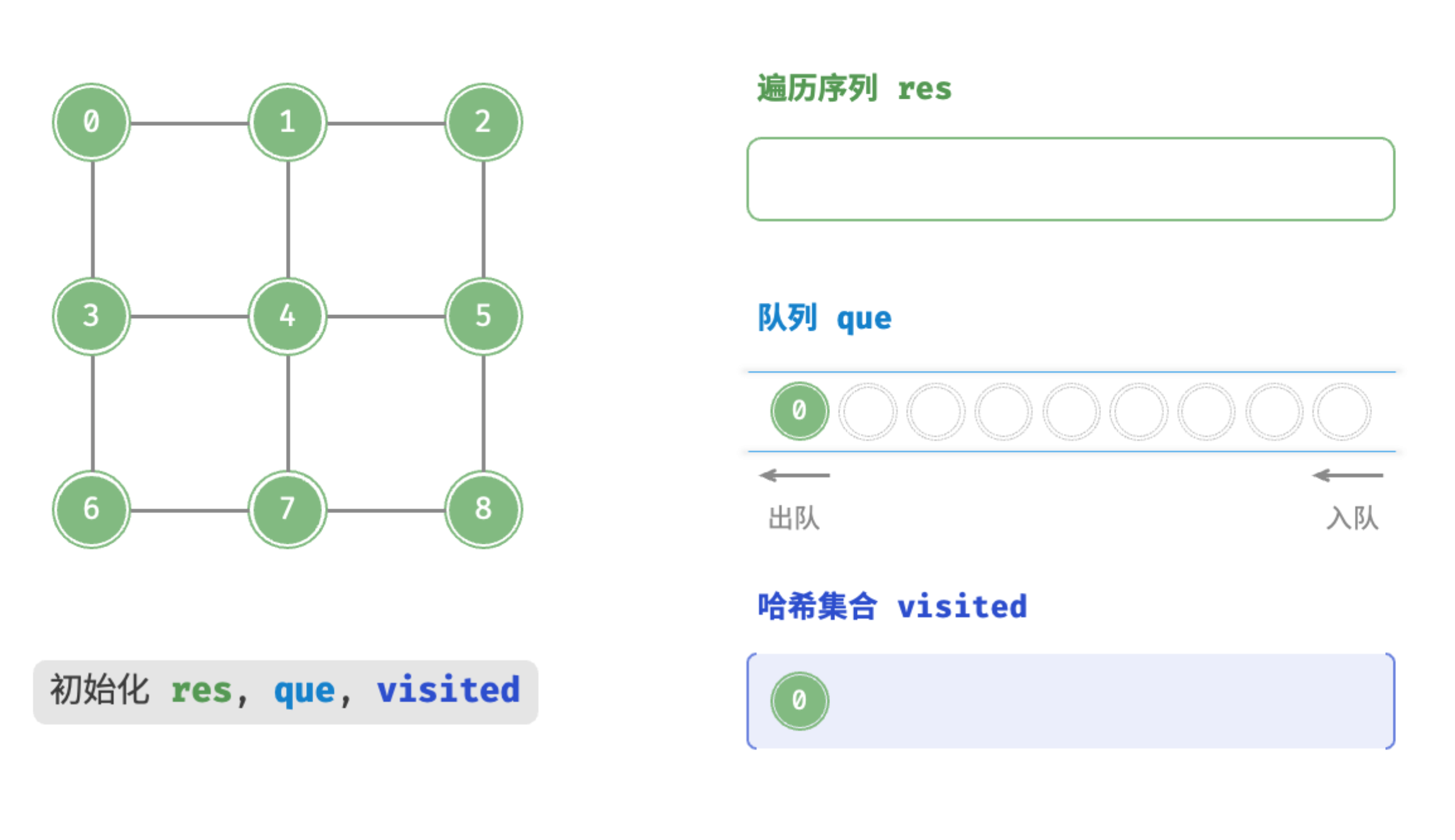
初始化res,que,visited
顶点0出队
顶点1出队
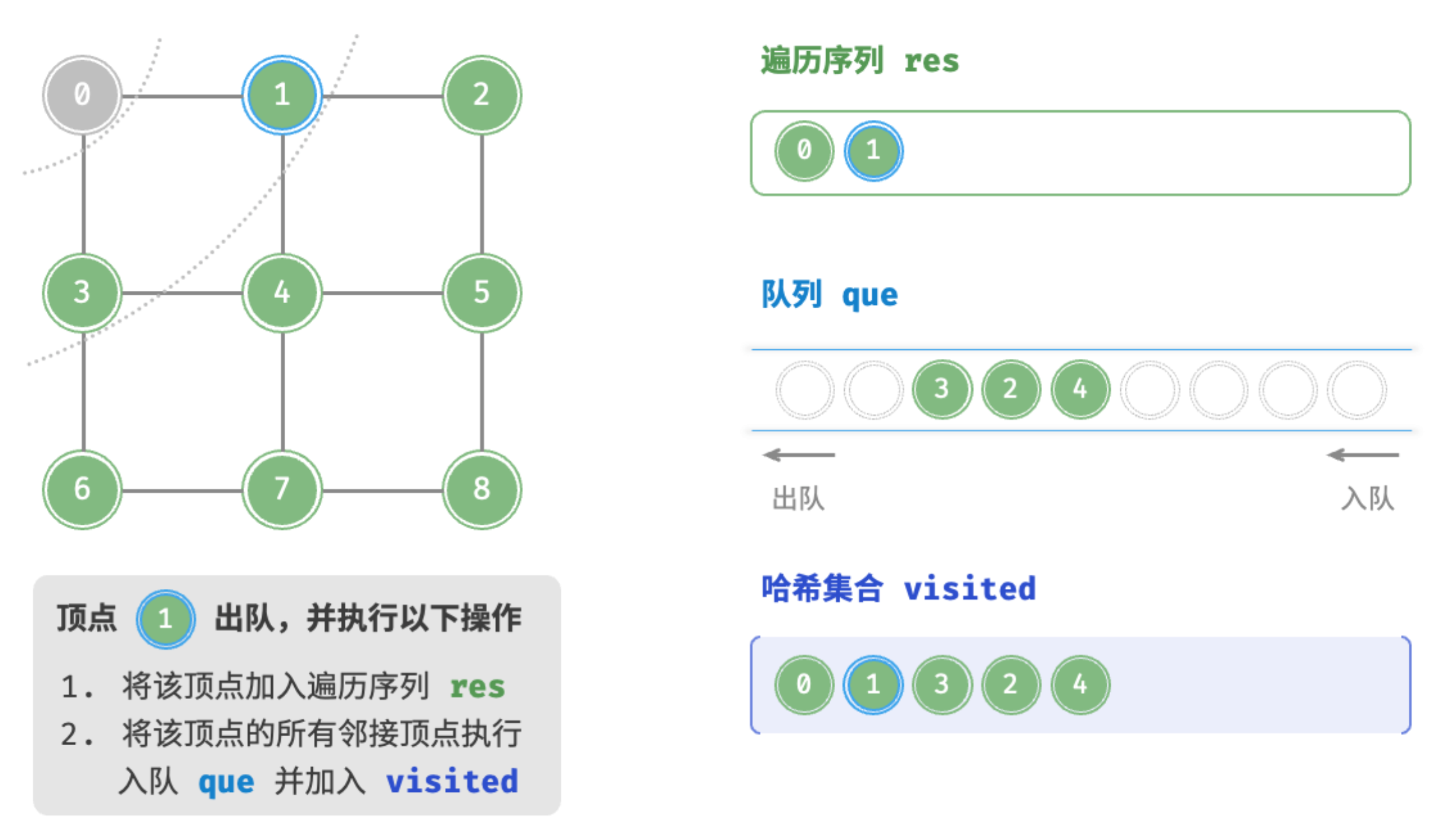
顶点3出队
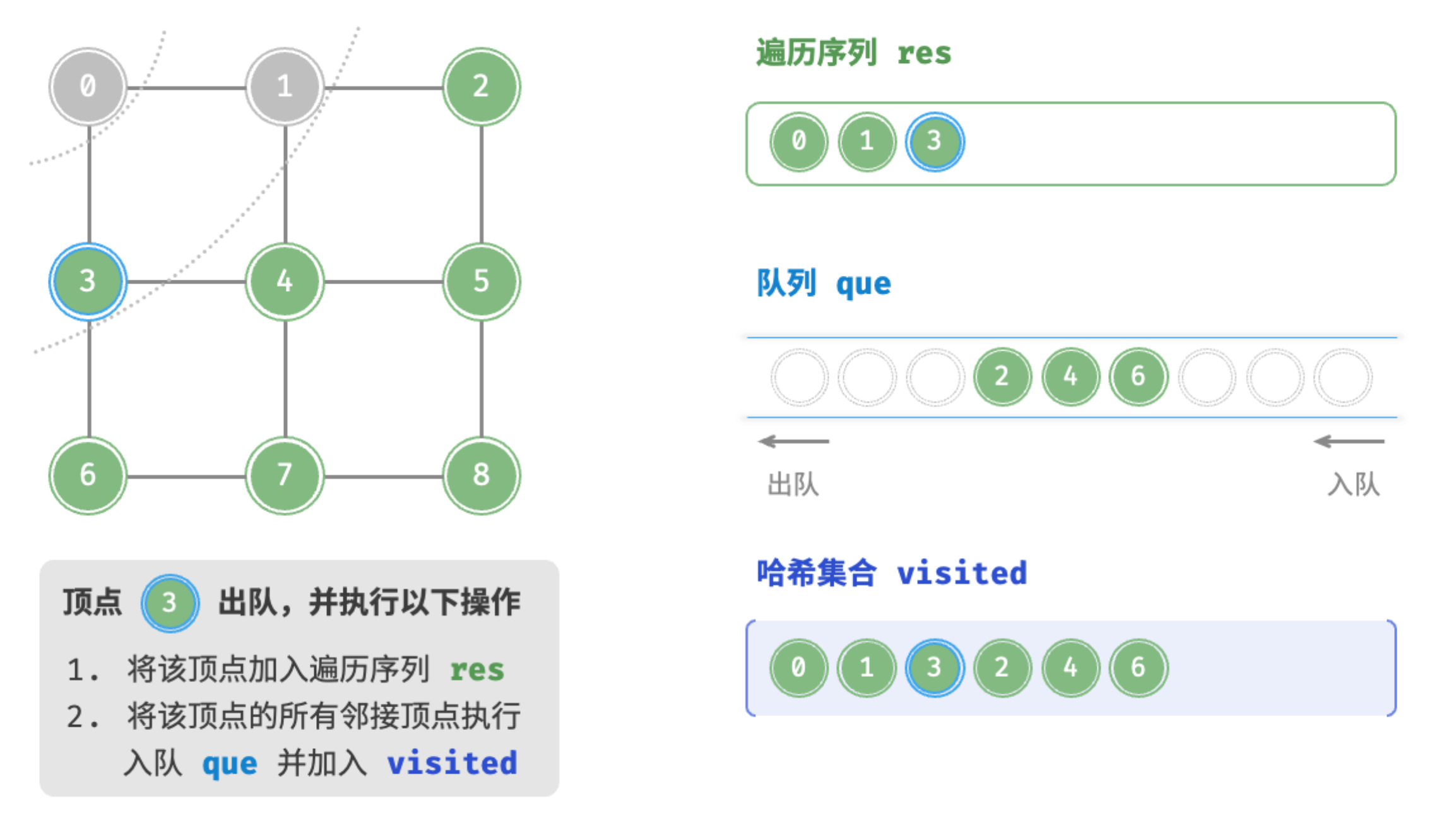
顶点2出队
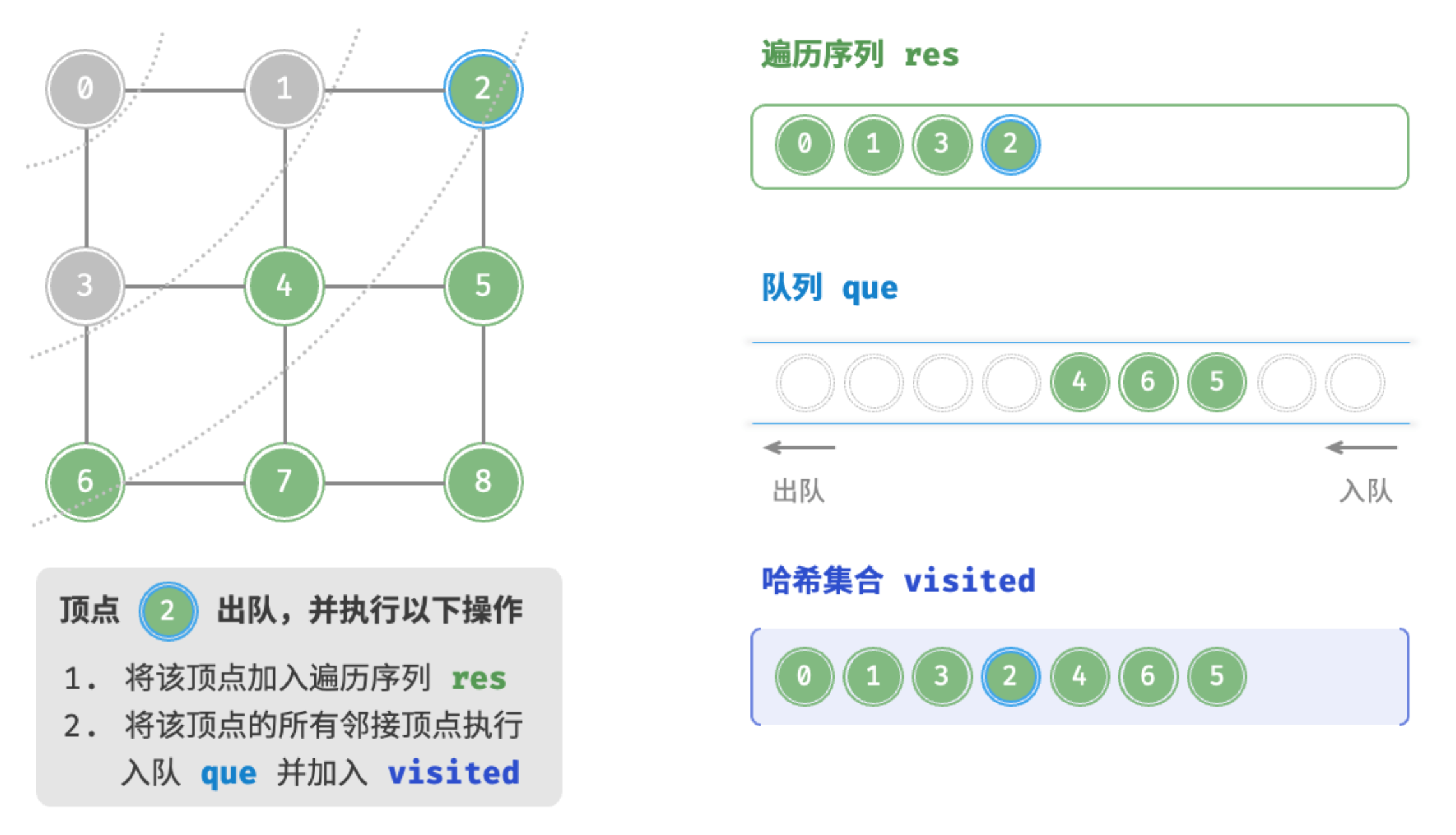
顶点4出队
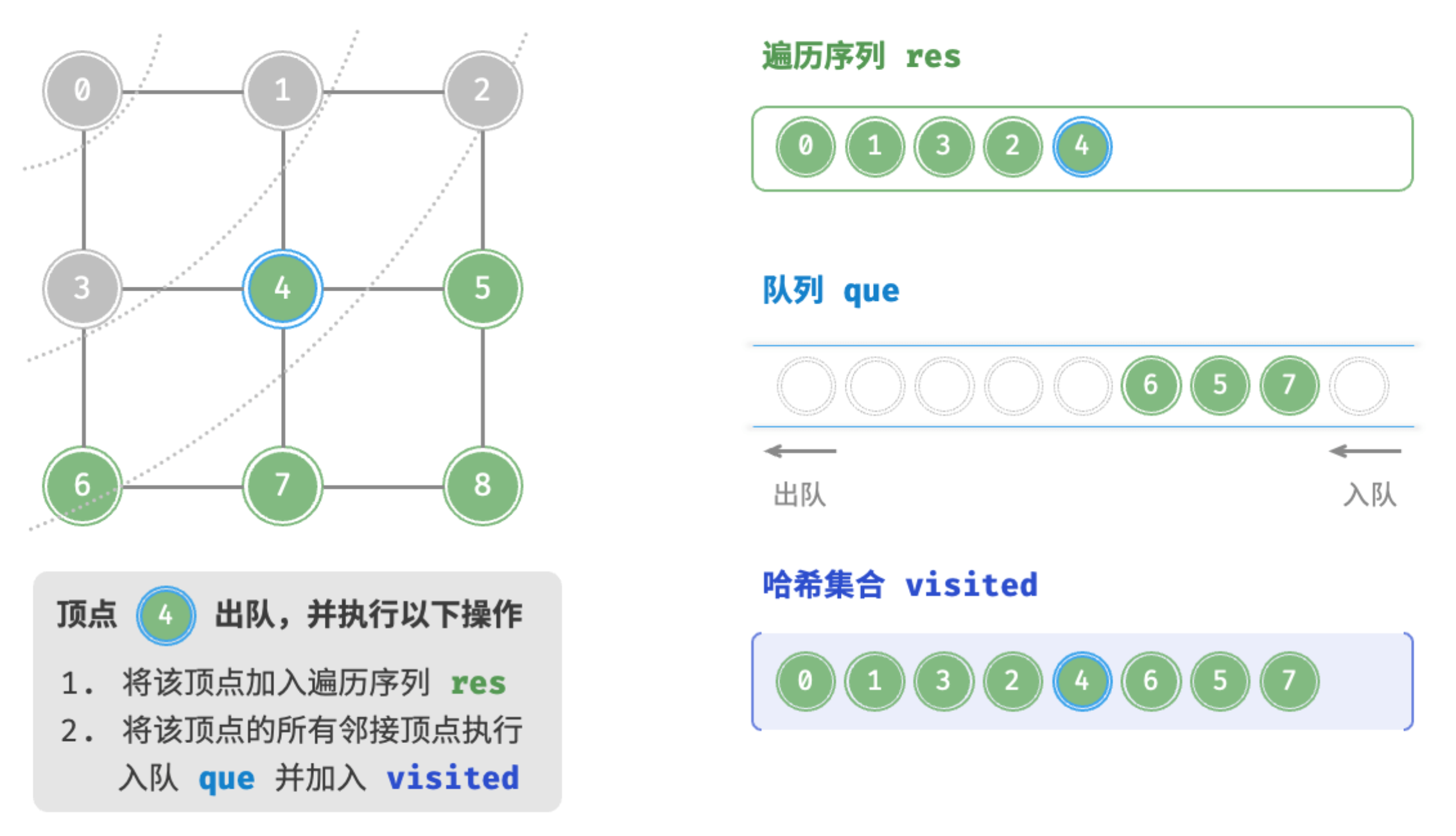
顶点6出队
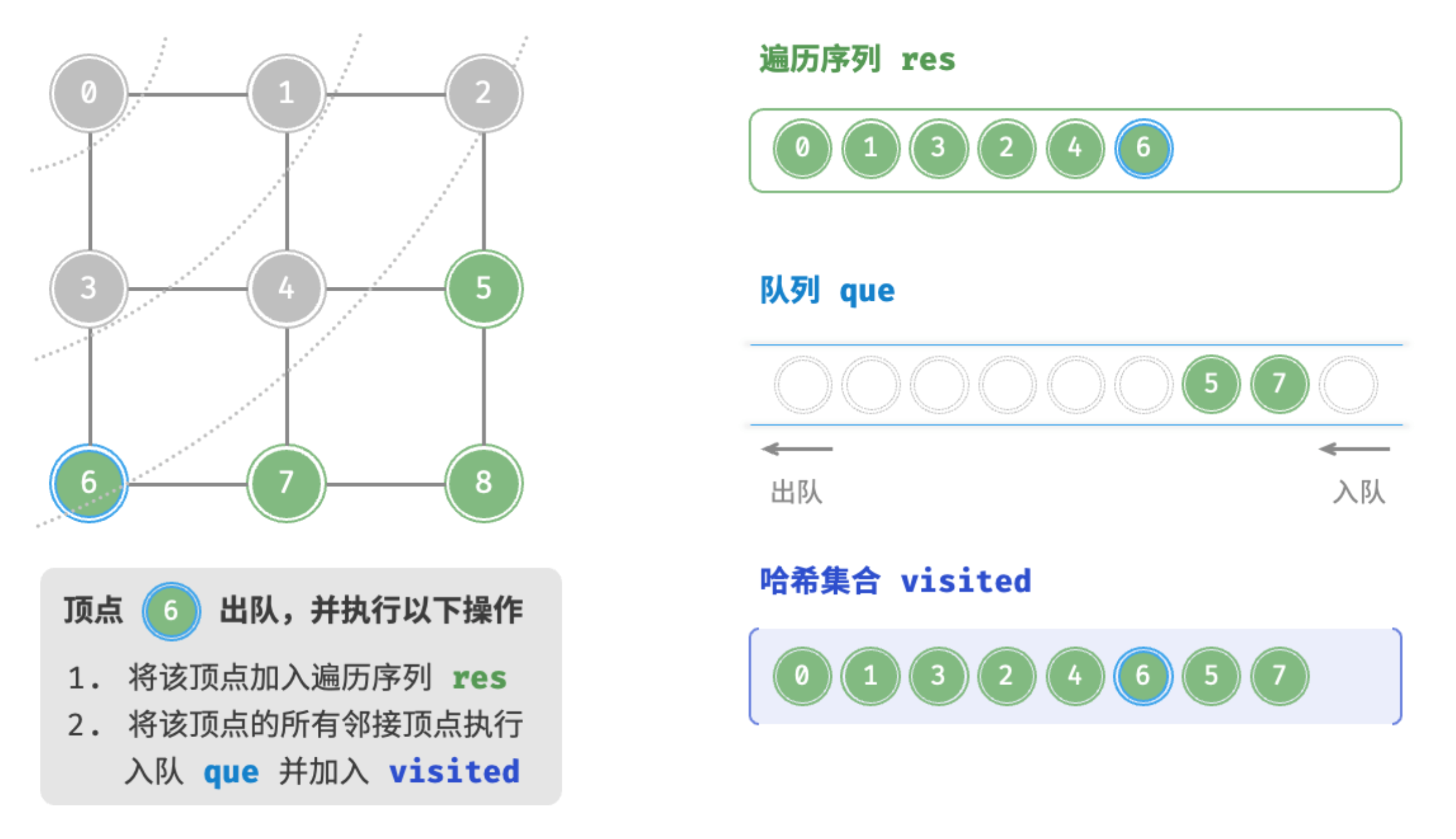
顶点5出队
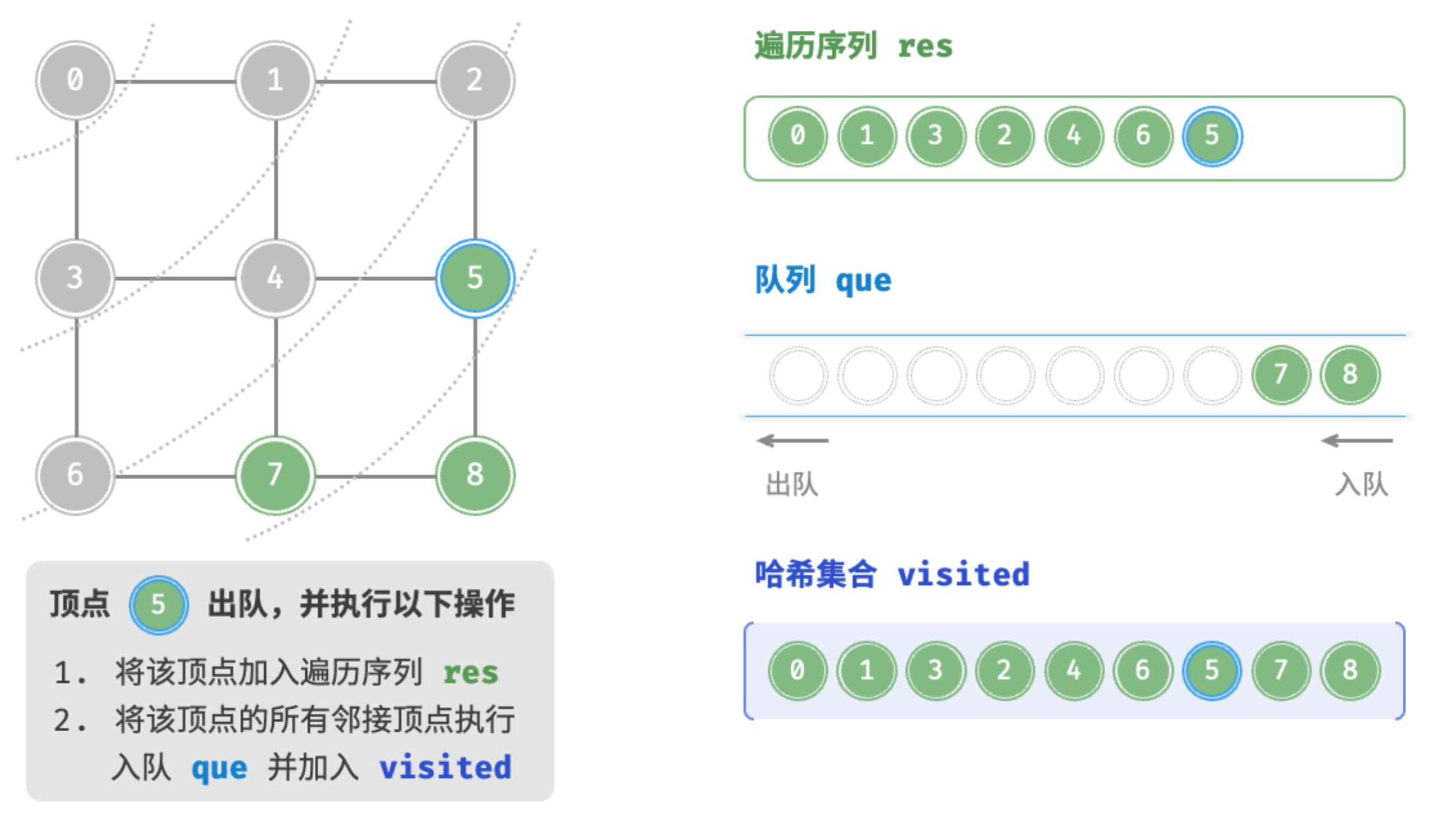
顶点7出队
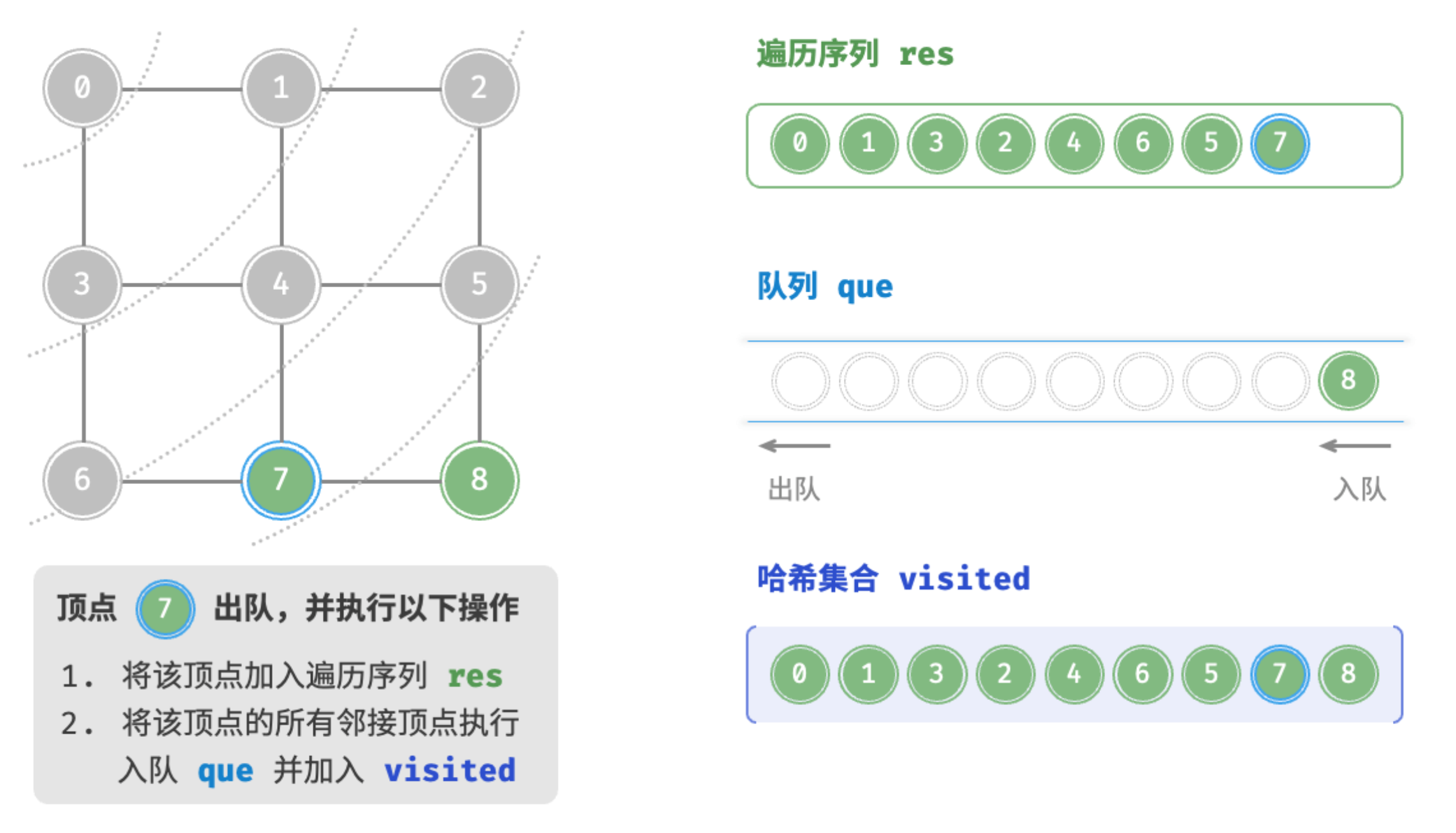
顶点8出队
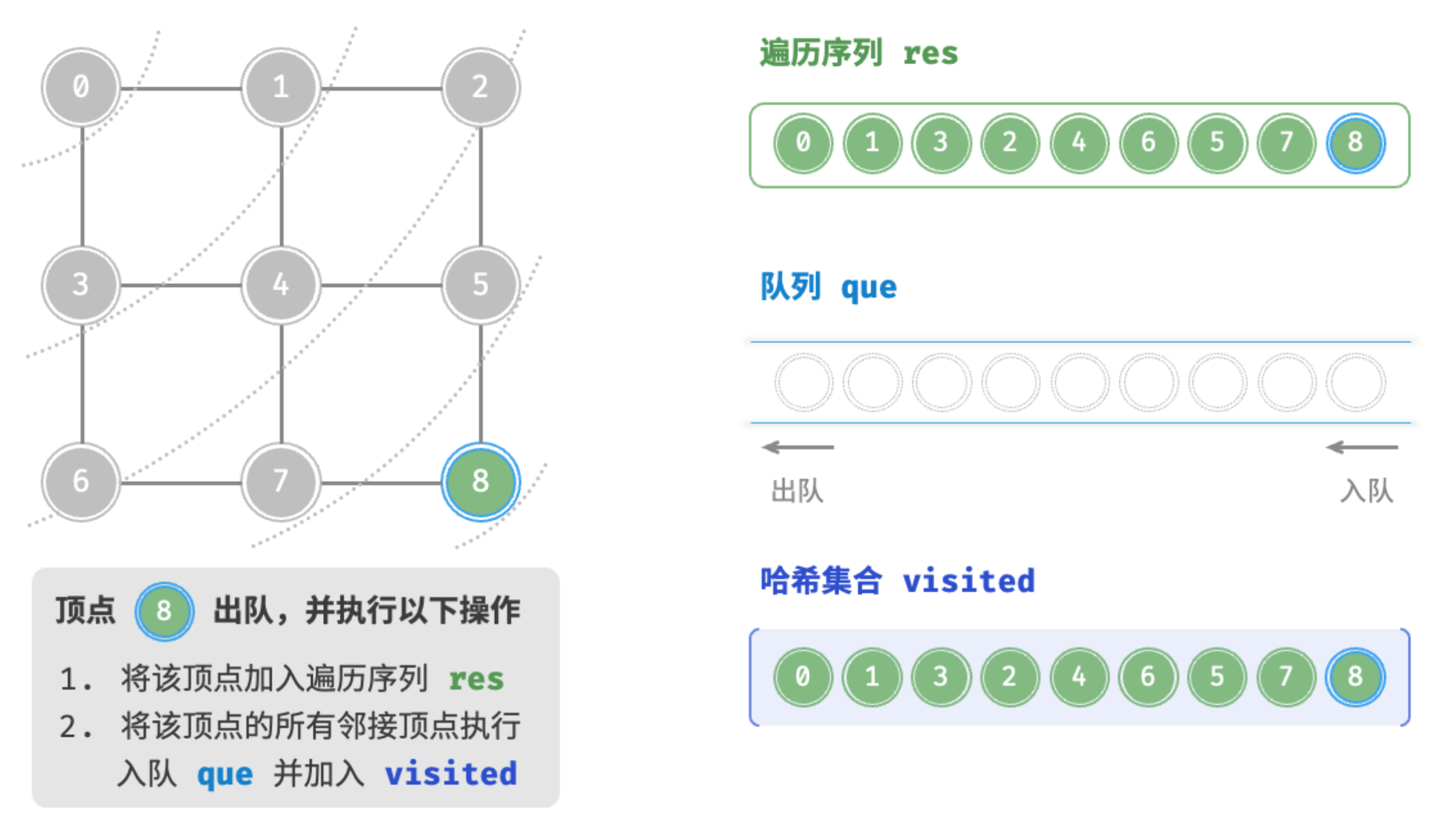
队列que为空
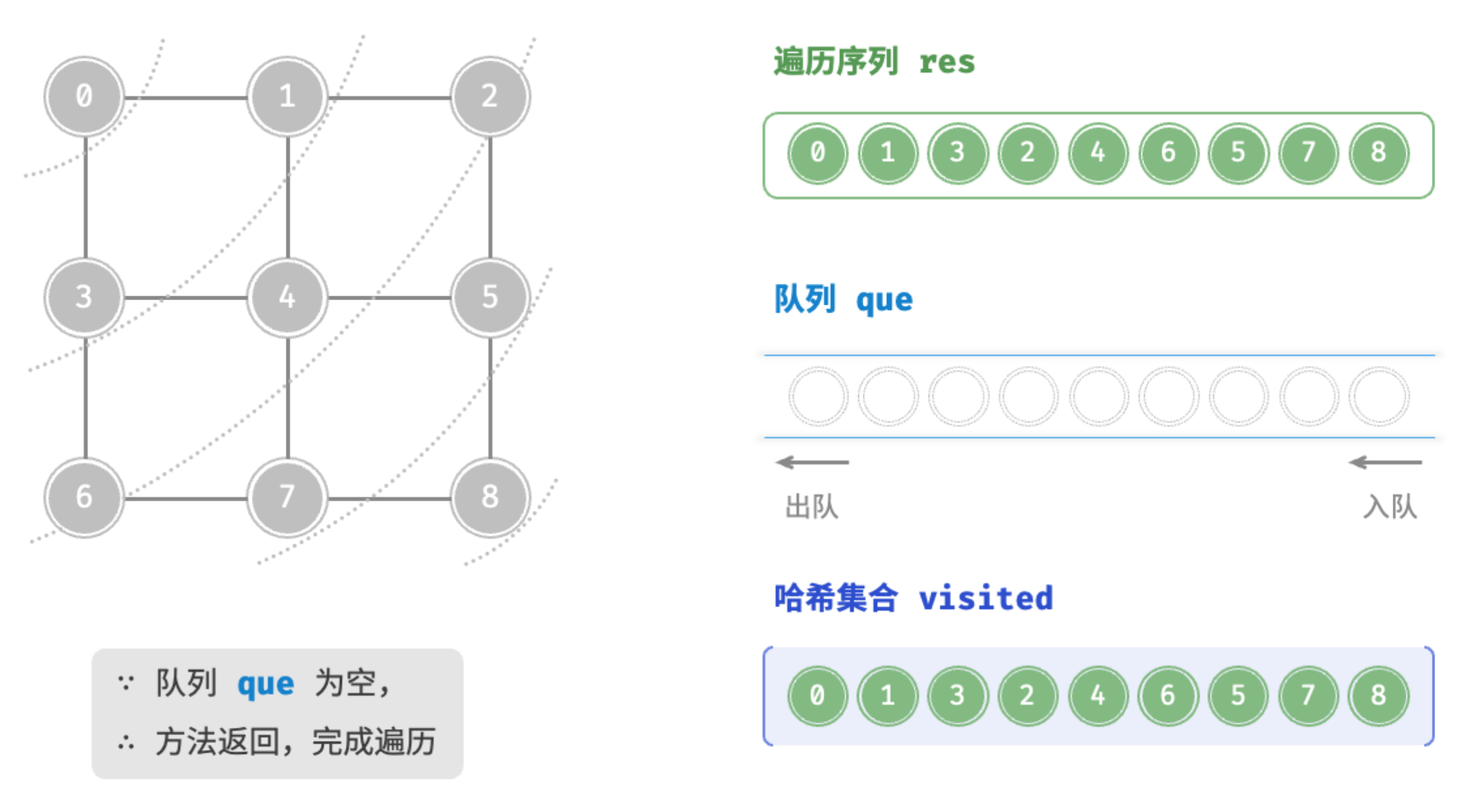
end
提示
广度优先遍历的序列是否唯一?
不唯一。广度优先遍历只要求按“由近及远”的顺序遍历,而多个相同距离的顶点的遍历顺序允许被任意打乱。以上图为例,顶点 1、3 的访问顺序可以交换,顶点 2、4、6 的访问顺序也可以任意交换。
复杂度分析
时间复杂度:所有顶点都会入队并出队一次,使用 O(∣V∣) 时间;在遍历邻接顶点的过程中,由于是无向图,因此所有边都会被访问 2 次,使用 O(2∣E∣) 时间;总体使用 O(∣V∣+∣E∣) 时间。
空间复杂度:列表
res,哈希集合visited,队列que中的顶点数量最多为 ∣V∣ ,使用 O(∣V∣) 空间。
深度优先遍历
深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。 如图所示,从左上角顶点出发,访问当前顶点的某个邻接顶点,直到走到尽头时返回,再继续走到尽头并返回,以此类推,直至所有顶点遍历完成。
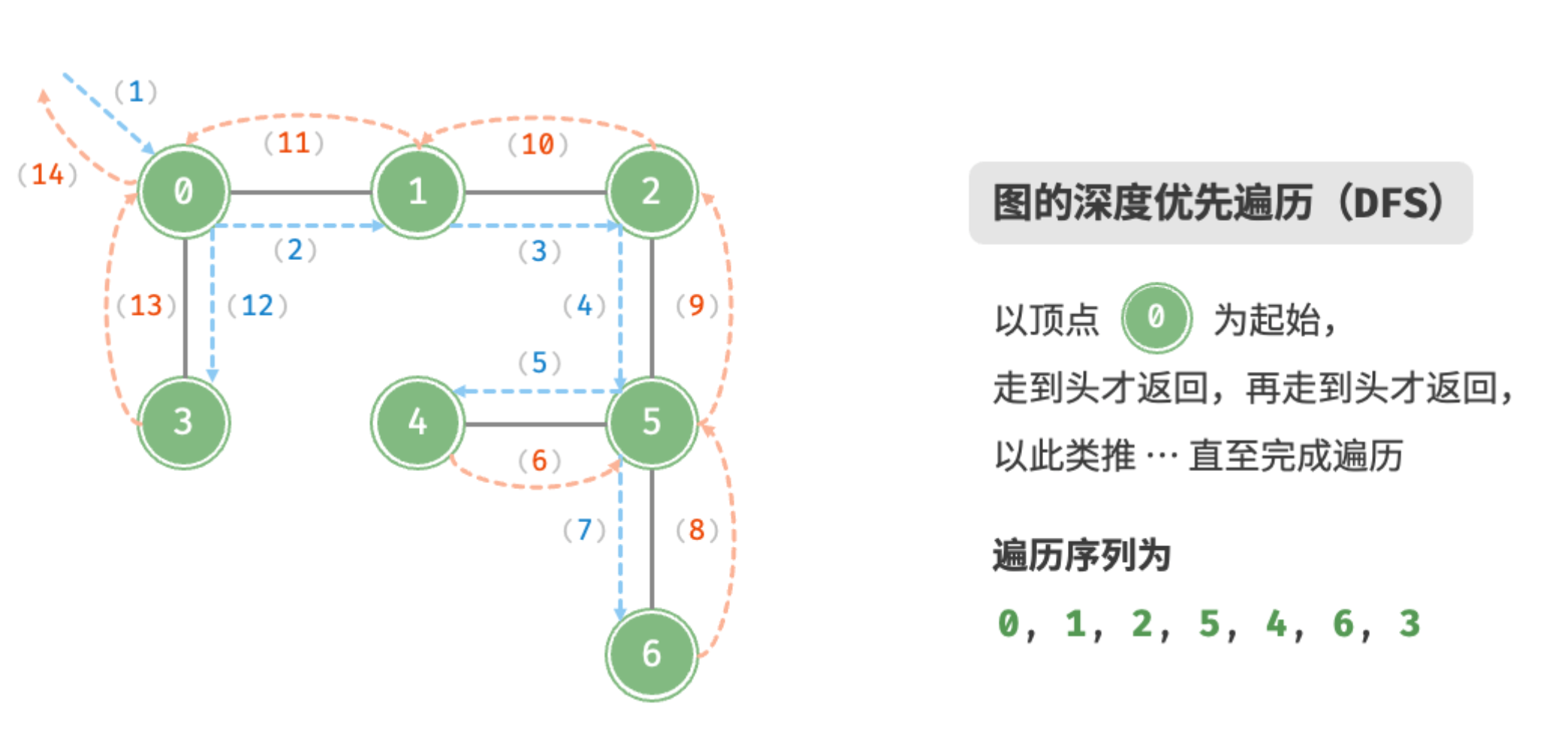
算法实现
这种“走到尽头再返回”的算法范式通常基于递归来实现。与广度优先遍历类似,在深度优先遍历中,我们也需要借助一个哈希集合 visited 来记录已被访问的顶点,以避免重复访问顶点。
/* 深度优先遍历辅助函数 */
func dfs(g *graphAdjList, visited map[Vertex]struct{}, res *[]Vertex, vet Vertex) {
// append 操作会返回新的的引用,必须让原引用重新赋值为新slice的引用
*res = append(*res, vet)
visited[vet] = struct{}{}
// 遍历该顶点的所有邻接顶点
for _, adjVet := range g.adjList[vet] {
_, isExist := visited[adjVet]
// 递归访问邻接顶点
if !isExist {
dfs(g, visited, res, adjVet)
}
}
}
/* 深度优先遍历 */
// 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点
func graphDFS(g *graphAdjList, startVet Vertex) []Vertex {
// 顶点遍历序列
res := make([]Vertex, 0)
// 哈希集合,用于记录已被访问过的顶点
visited := make(map[Vertex]struct{})
dfs(g, visited, &res, startVet)
// 返回顶点遍历序列
return res
}深度优先遍历的算法流程如下图所示。
- 直虚线代表向下递推,表示开启了一个新的递归方法来访问新顶点。
- 曲虚线代表向上回溯,表示此递归方法已经返回,回溯到了开启此方法的位置。
为了加深理解,建议将图与代码结合起来,在脑中模拟(或者用笔画下来)整个 DFS 过程,包括每个递归方法何时开启、何时返回。
递推阶段:访问顶点0
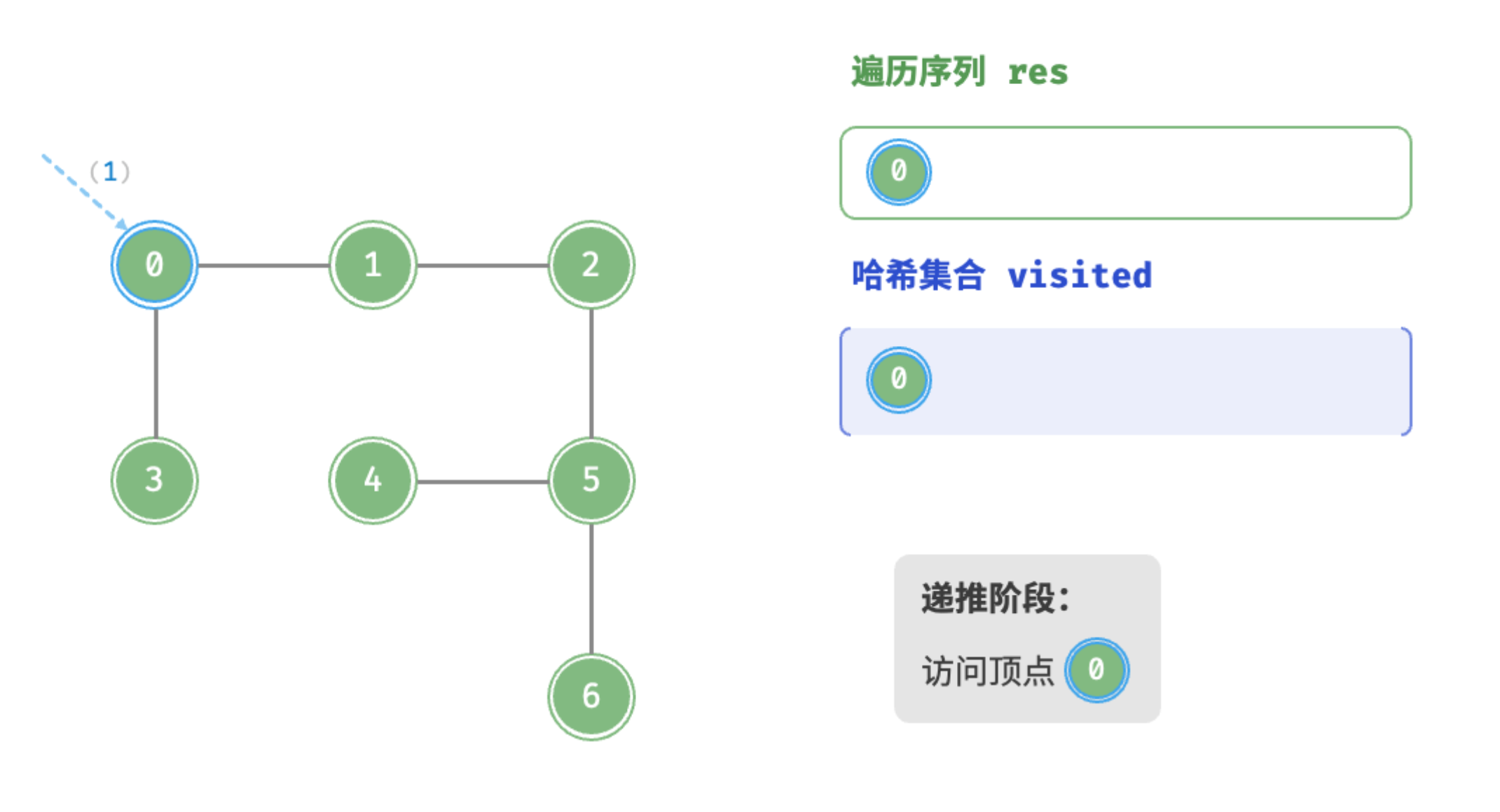
递推阶段:访问顶点0的邻接顶点,递归访问顶点1
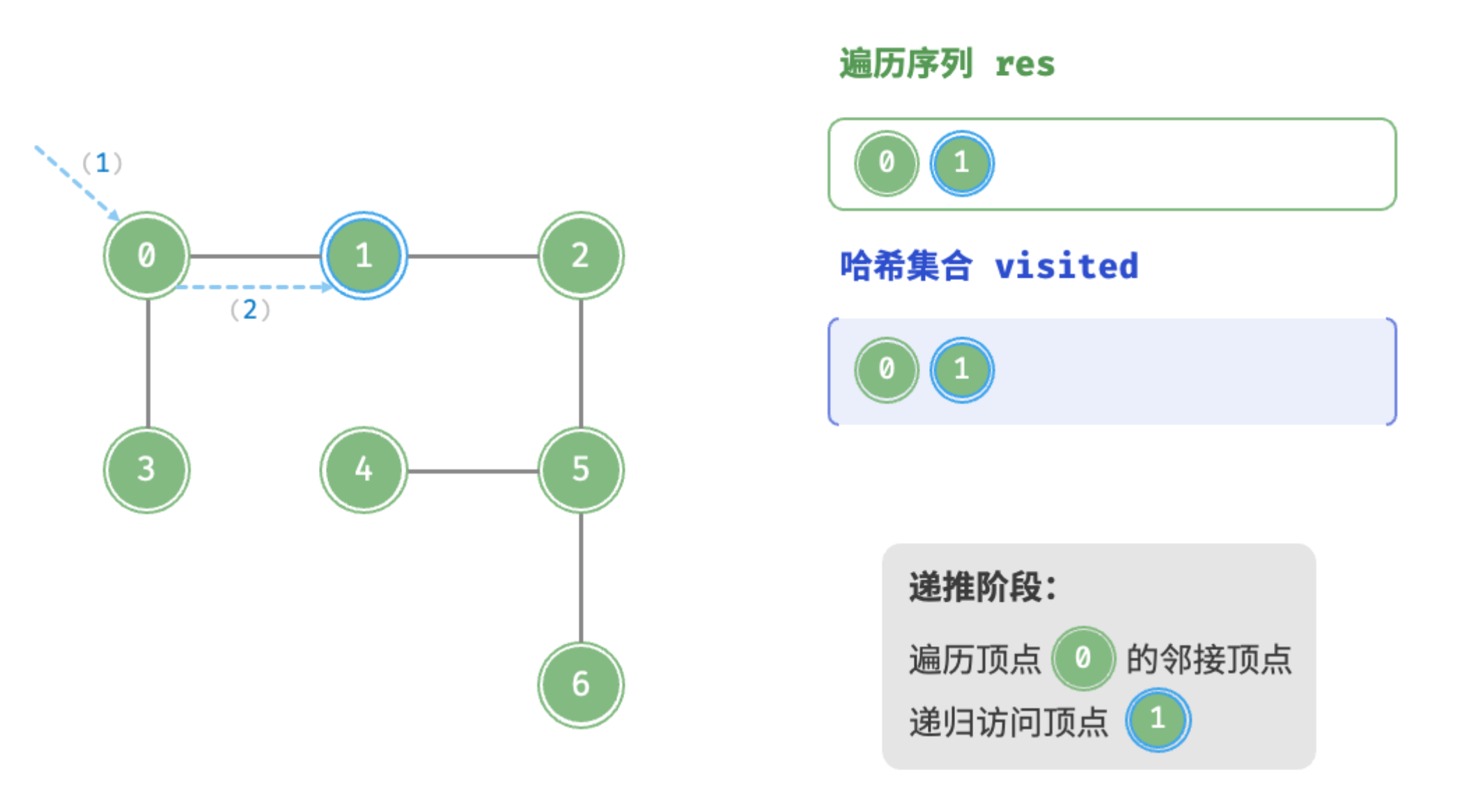
递推阶段:访问顶点1的邻接顶点,递归访问顶点2
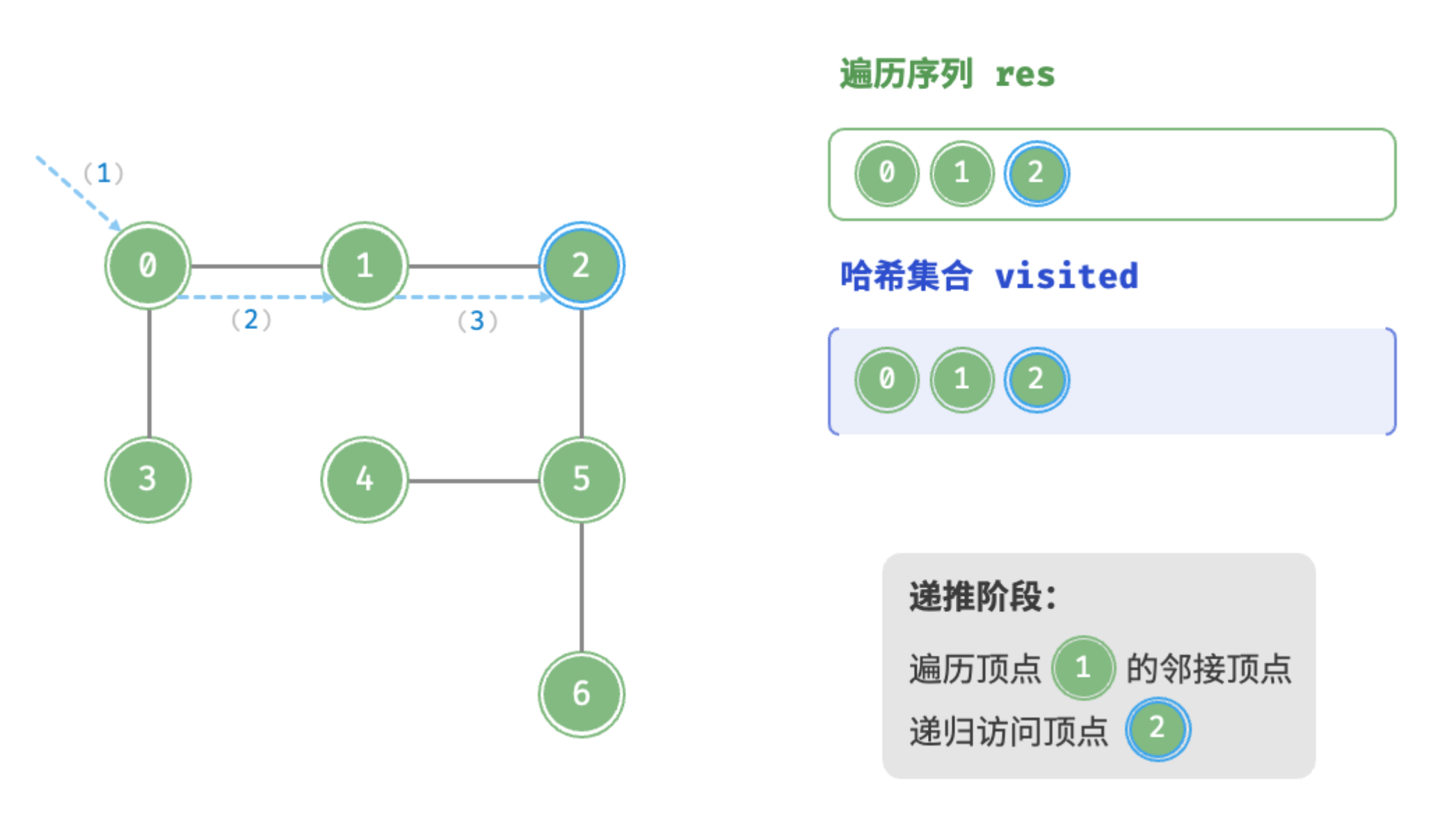
递推阶段:访问顶点2的邻接顶点,递归访问顶点5
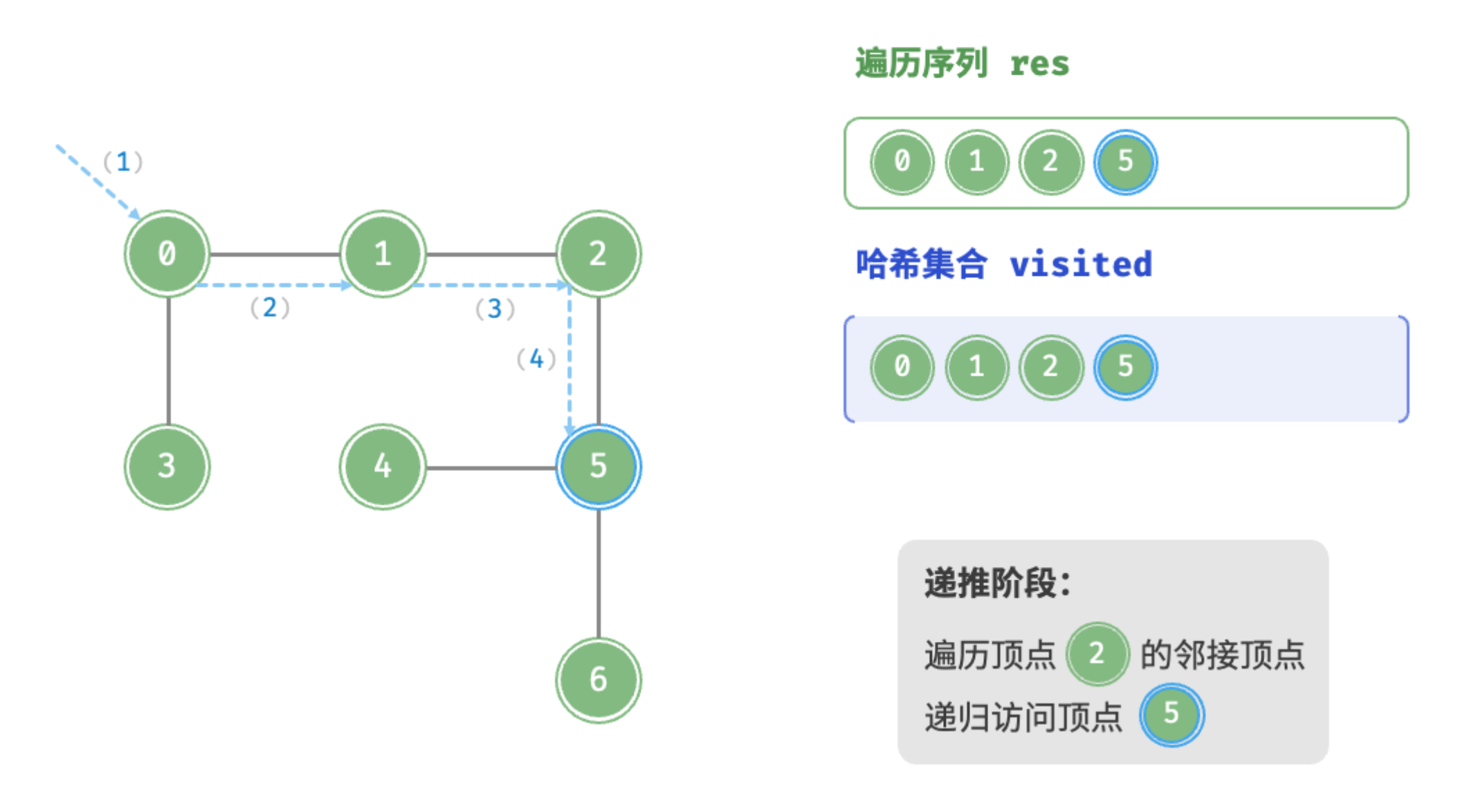
递推阶段:访问顶点5的邻接顶点,递归访问顶点4
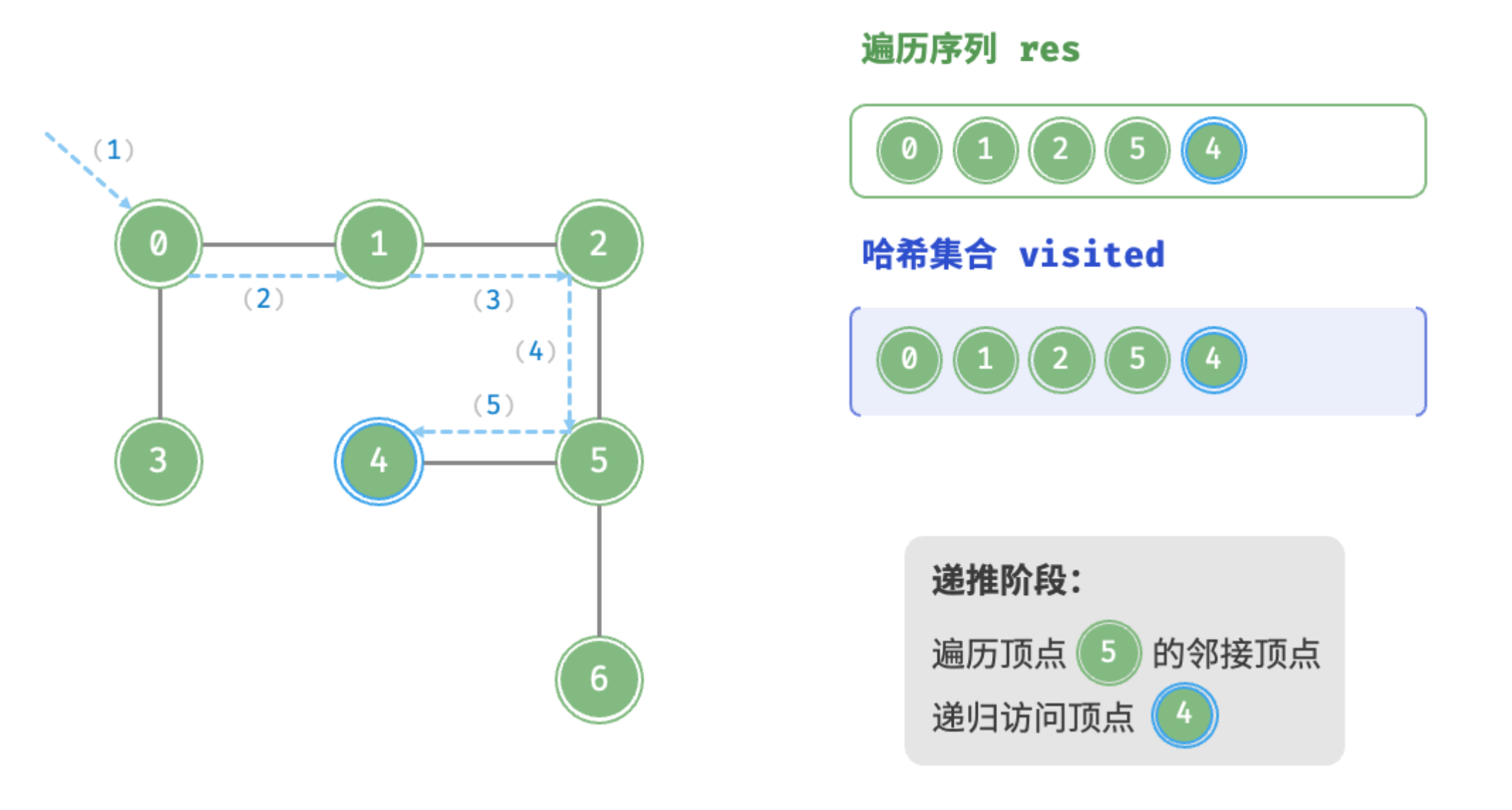
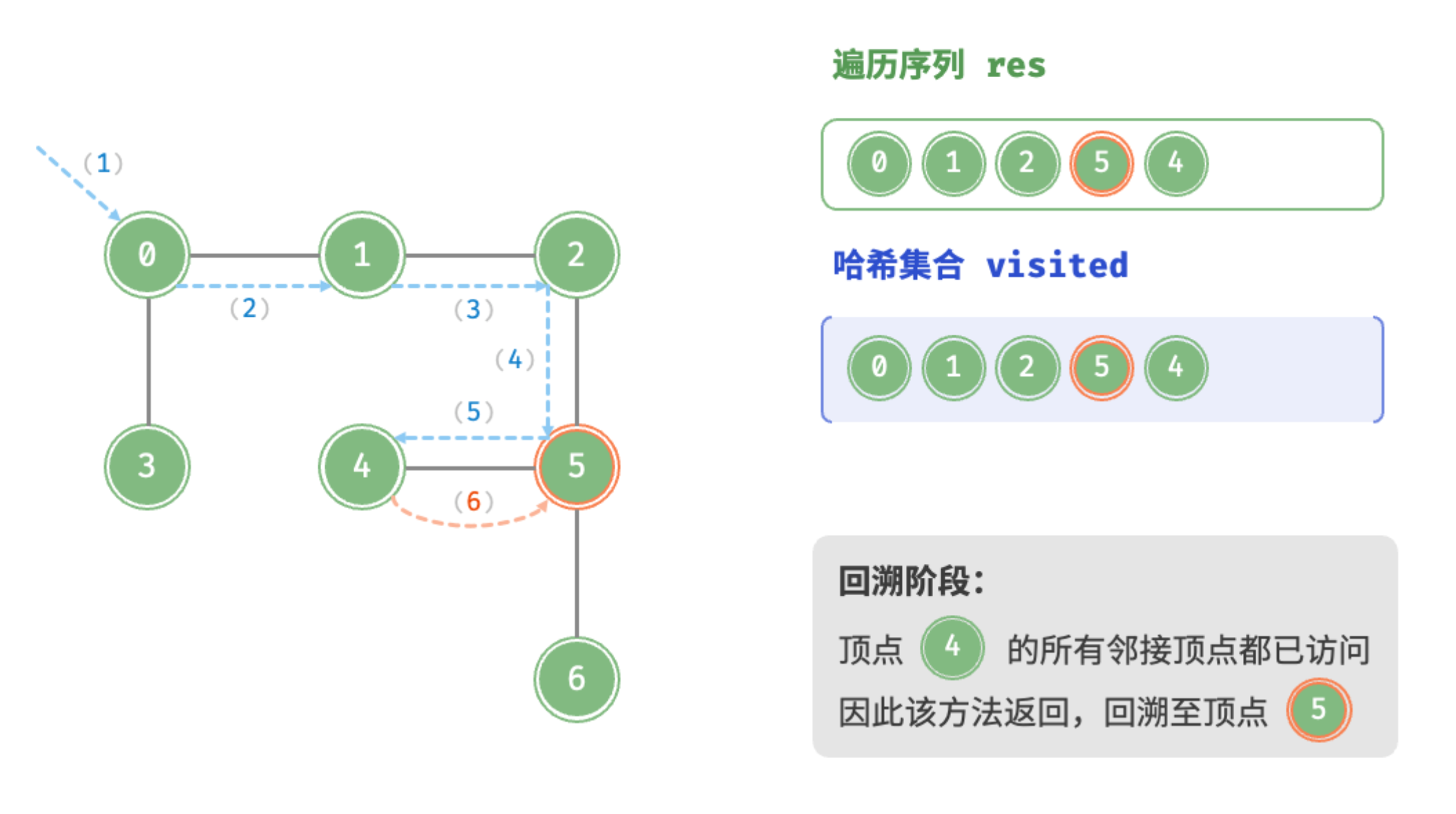
回溯阶段:顶点4的所有邻接顶点都已访问,回溯至顶点5
递推阶段:遍历顶点5的邻接顶点,递归访问顶点6
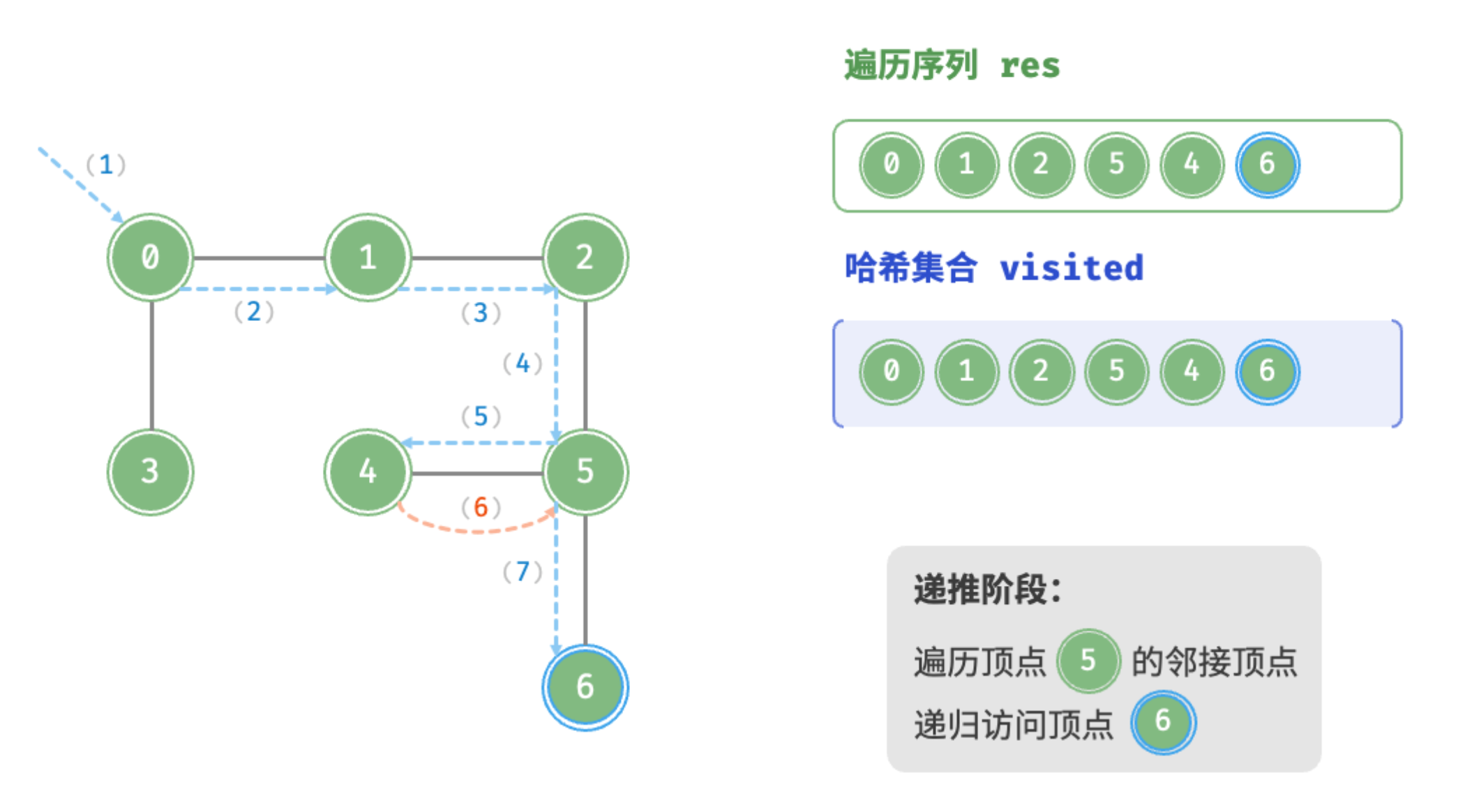
回溯阶段:顶点6的所有邻接顶点都已访问,回溯至顶点5
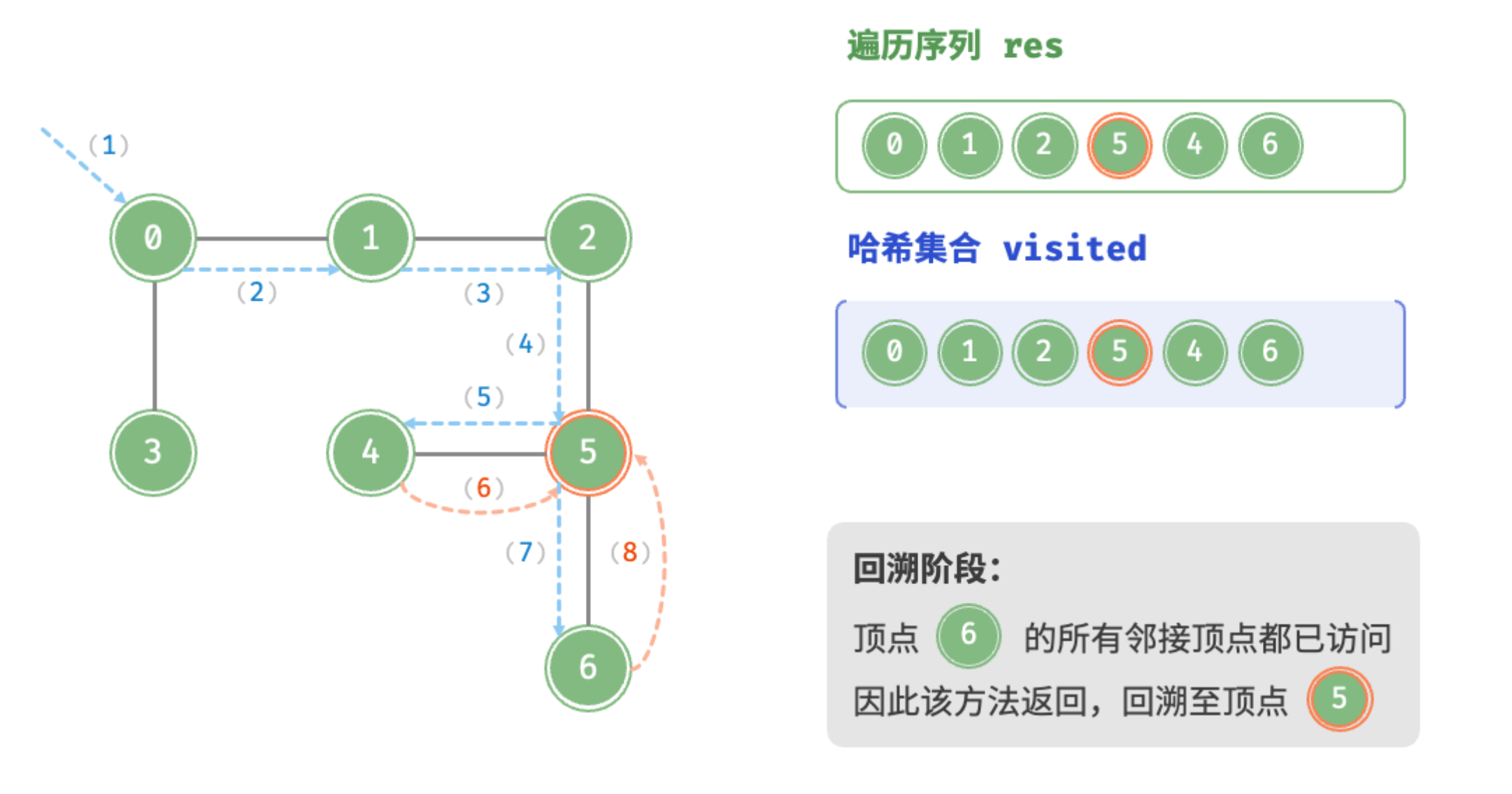
回溯阶段:顶点6的所有邻接顶点都已访问,回溯至顶点5,以此类推,最终回溯至顶点0
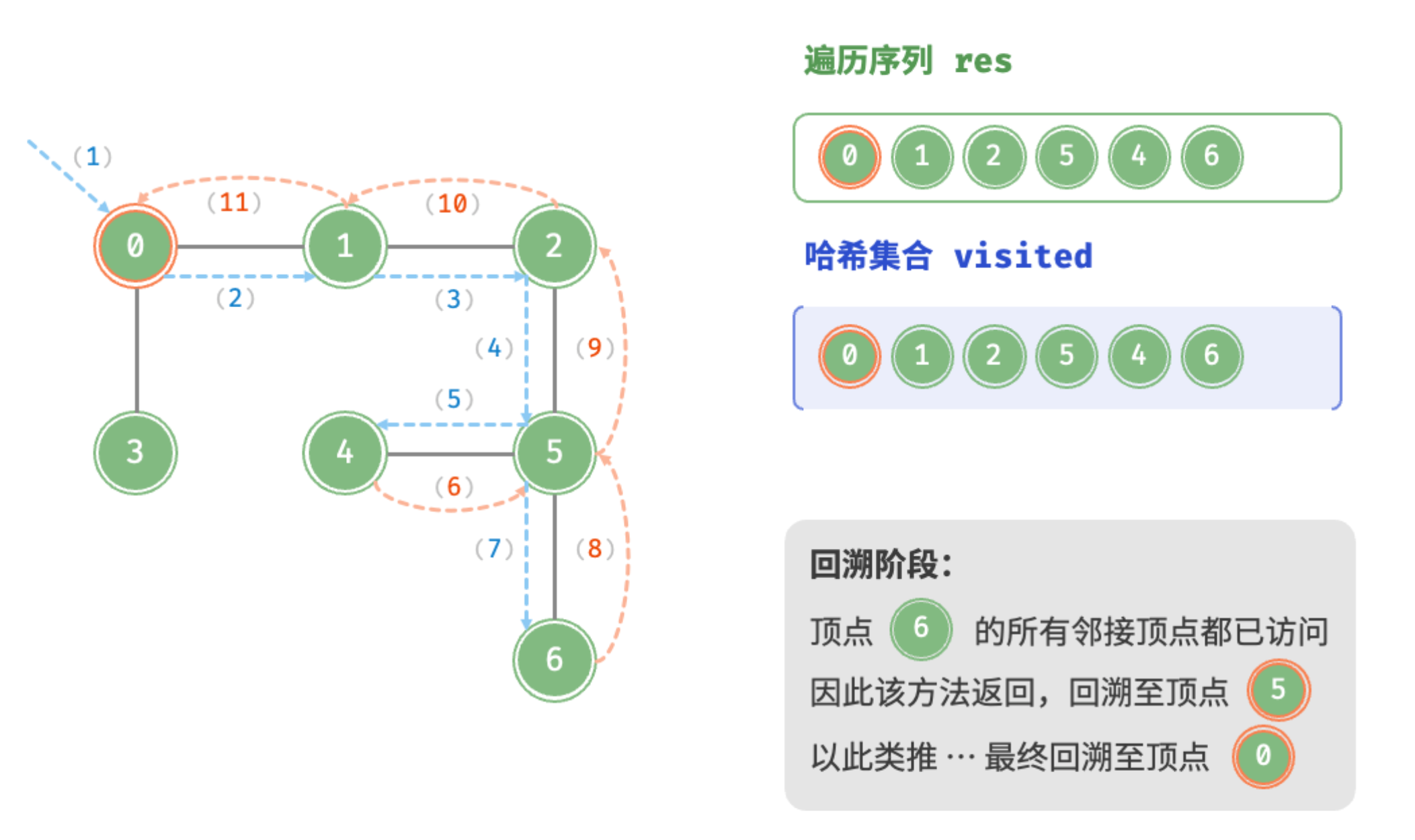
递推阶段:遍历顶点0的邻接顶点,递归访问顶点3
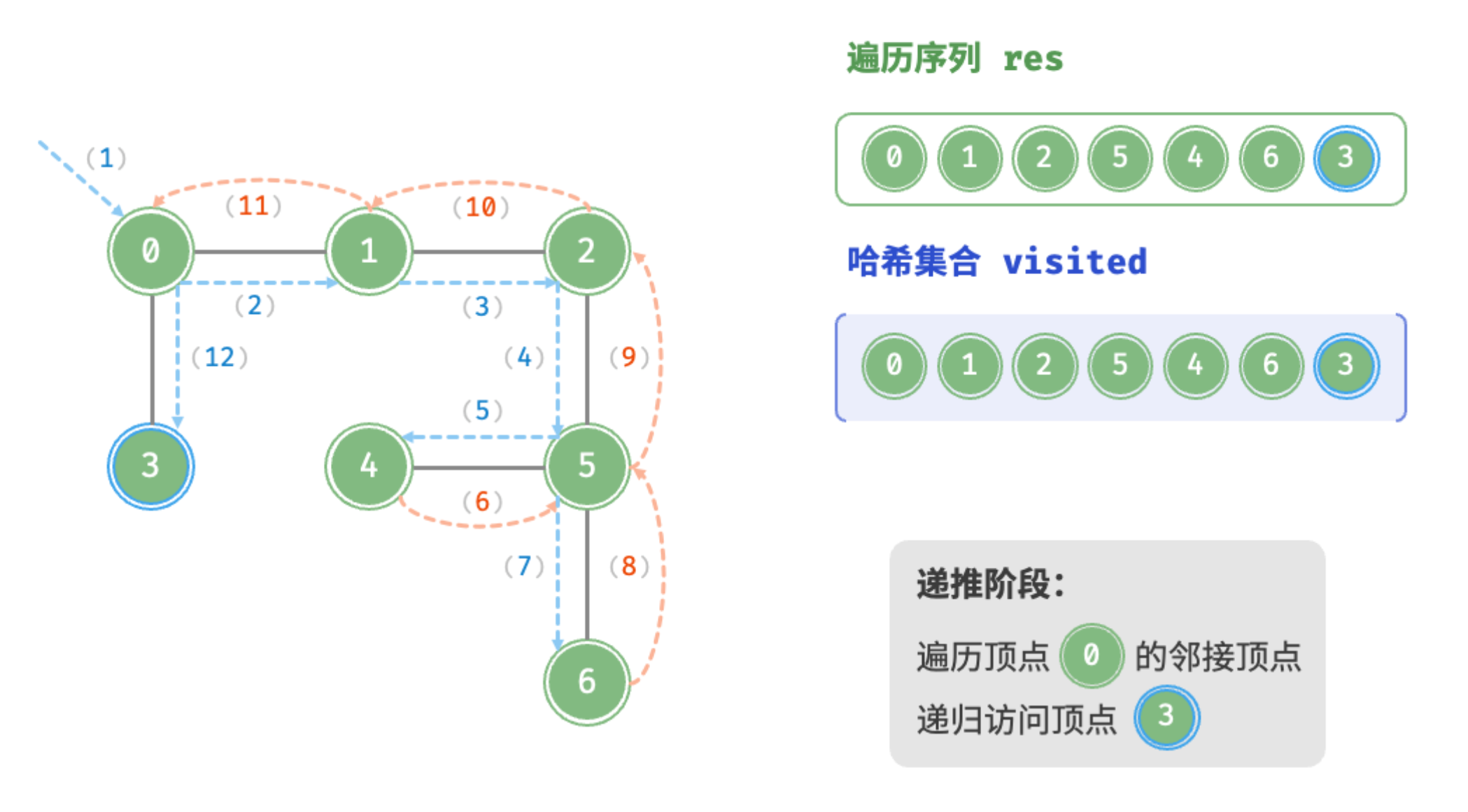
回溯阶段:顶点3的所有邻接顶点都已访问,回溯至顶点0,完成遍历
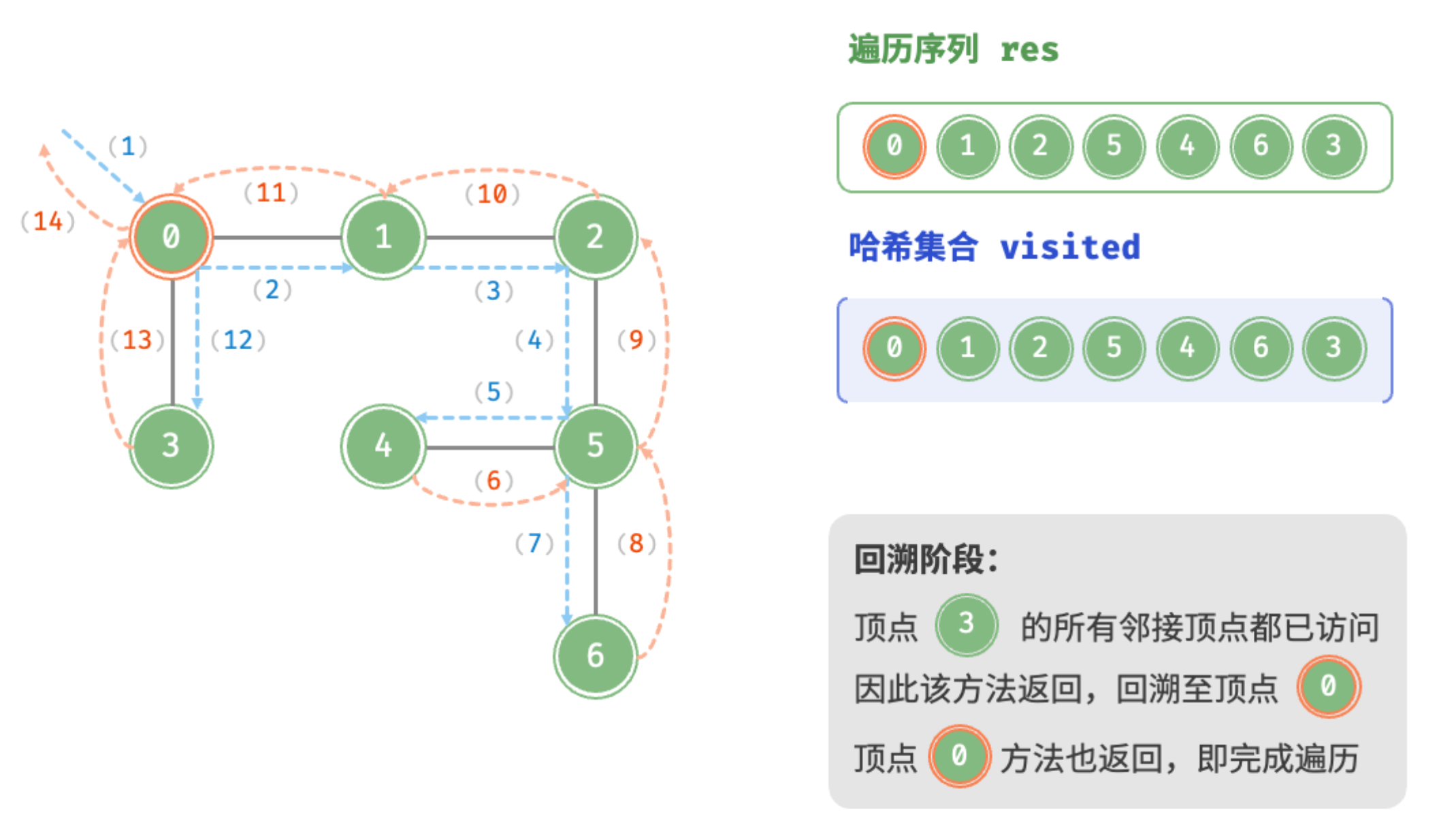
end
提示
深度优先遍历的序列是否唯一?
与广度优先遍历类似,深度优先遍历序列的顺序也不是唯一的。给定某顶点,先往哪个方向探索都可以,即邻接顶点的顺序可以任意打乱,都是深度优先遍历。
以树的遍历为例,“根 -> 左 -> 右”“左 -> 根 -> 右”“左 -> 右 -> 根”分别对应前序、中序、后序遍历,它们展示了三种遍历优先级,然而这三者都属于深度优先遍历。
复杂度分析
时间复杂度:所有顶点都会被访问 1 次,使用 O(∣V∣) 时间;所有边都会被访问 2 次,使用 O(2∣E∣) 时间;总体使用 O(∣V∣+∣E∣) 时间。
空间复杂度:列表 res ,哈希集合 visited 顶点数量最多为 ∣V∣ ,递归深度最大为 V ,因此使用 O(∣V∣) 空间。
小结
- 图由顶点和边组成,可以表示为一组顶点和一组边构成的集合。
- 相较于线性关系(链表)和分治关系(树),网络关系(图)具有更高的自由度,因而更为复杂。
- 有向图的边具有方向性,连通图中的任意顶点均可达,有权图的每条边都包含权重变量。
- 邻接矩阵利用矩阵来表示图,每一行(列)代表一个顶点,矩阵元素代表边,用 1 或 0 表示两个顶点之间有边或无边。邻接矩阵在增删查改操作上效率很高,但空间占用较多。
- 邻接表使用多个链表来表示图,第 i 个链表对应顶点 i ,其中存储了该顶点的所有邻接顶点。邻接表相对于邻接矩阵更加节省空间,但由于需要遍历链表来查找边,因此时间效率较低。
- 当邻接表中的链表过长时,可以将其转换为红黑树或哈希表,从而提升查询效率。
- 从算法思想的角度分析,邻接矩阵体现了“以空间换时间”,邻接表体现了“以时间换空间”。
- 图可用于建模各类现实系统,如社交网络、地铁线路等。
- 树是图的一种特例,树的遍历也是图的遍历的一种特例。
- 图的广度优先遍历是一种由近及远、层层扩张的搜索方式,通常借助队列实现。
- 图的深度优先遍历是一种优先走到底、无路可走时再回溯的搜索方式,常基于递归来实现。